Bảng tổng hợp các công thức lượng giác được biên soạn một cách khoa học và ngắn gọn, giúp học sinh dễ dàng nắm bắt và áp dụng hiệu quả vào các dạng bài tập liên quan. Hãy tham khảo ngay để học tốt hơn!
1. Khái niệm cơ bản về lượng giác
Lượng giác là một lĩnh vực toán học nghiên cứu mối quan hệ giữa các góc và các cạnh của tam giác, đặc biệt là tam giác vuông. Các hàm lượng giác cơ bản gồm:
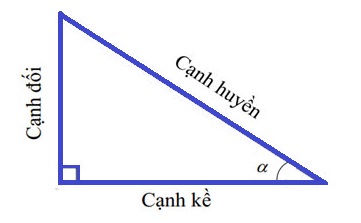
- (\(\sin\)): Tỉ số giữa cạnh đối và cạnh huyền ⇒ $\sin \theta = \frac{\text{Cạnh đối}}{\text{Cạnh huyền}}$
- (\(\cos\)): Tỉ số giữa cạnh kề và cạnh huyền ⇒ $\cos \theta = \frac{\text{Cạnh kề}}{\text{Cạnh huyền}}$
- (\(\tan\)): Tỉ số giữa cạnh đối và cạnh kề ⇒ $\tan \theta = \frac{\text{Cạnh đối}}{\text{Cạnh kề}}$
- (\(\cot\)): Tỉ số giữa cạnh kề và cạnh đối ⇒ $\cot \theta = \frac{\text{Cạnh kề}}{\text{Cạnh đối}}$
2. Các công thức lượng giác cơ bản
2.1. Các công thức lượng giác cơ bản
Hệ thức cơ bản: $\sin^2 \theta + \cos^2 \theta = 1.$
Từ đó suy ra: $\tan^2 \theta + 1 = \sec^2 \theta, \quad 1 + \cot^2 \theta = \csc^2 \theta.$
Công thức cộng:
- $\sin(a + b) = \sin a \cos b + \cos a \sin b. $
- $\cos(a + b) = \cos a \cos b – \sin a \sin b. $
- $\tan(a + b) = \frac{\tan a + \tan b}{1 – \tan a \tan b} \quad (\text{với } \tan a \tan b \neq 1). $
Công thức trừ:
- $\sin(a – b) = \sin a \cos b – \cos a \sin b. $
- $\cos(a – b) = \cos a \cos b + \sin a \sin b. $
- $\tan(a – b) = \frac{\tan a – \tan b}{1 + \tan a \tan b}. $
Để nhớ lâu bạn có thể học thuộc bài thơ sau:
Công thức lượng giác nhớ hoài,
Cos cộng cos, hai cos nhân nhau dài,
Cos trừ cos, sin sin mang dấu trừ,
Sin cộng sin, hai sin cos chẳng dư,
Sin trừ sin, cos sin nhân số hai.
Sin tổng thì, sin cos cộng cos sin,
Sin hiệu thì, sin cos trừ cos sin,
Cos tổng thì, cos cos trừ sin sin,
Cos hiệu thì, cos cos cộng sin sin.
Tang tổng kia, tang cộng tang thật ngon,
Chia một trừ tích tang, nhớ luôn trong lòng,
Học công thức, nhẹ nhàng như hát ca,
Lượng giác này, nhớ mãi chẳng phai xa.
2.2 Công thức các cung liên kết trên đường tròn lượng giác
Công thức đối xứng qua gốc tọa độ (góc đối):
- $ \sin(-x) = -\sin(x) $
- $ \cos(-x) = \cos(x) $
- $ \tan(-x) = -\tan(x) $
- $ \cot(-x) = -\cot(x) $
Công thức đối xứng qua trục hoành (góc bù):
- $ \sin(\pi – x) = \sin(x) $
- $ \cos(\pi – x) = -\cos(x) $
- $ \tan(\pi – x) = -\tan(x) $
- $ \cot(\pi – x) = -\cot(x) $
Công thức đối xứng qua trục tung (góc phụ):
- $ \sin\left(\frac{\pi}{2} – x\right) = \cos(x) $
- $ \cos\left(\frac{\pi}{2} – x\right) = \sin(x) $
- $ \tan\left(\frac{\pi}{2} – x\right) = \cot(x) $
- $ \cot\left(\frac{\pi}{2} – x\right) = \tan(x) $
Công thức đối xứng qua tâm đường tròn (góc hơn kém \( \pi \)):
- $ \sin(\pi + x) = -\sin(x) $
- $ \cos(\pi + x) = -\cos(x) $
- $ \tan(\pi + x) = \tan(x) $
- $ \cot(\pi + x) = \cot(x) $
Công thức bổ sung (góc hơn kém \( 2\pi \)):
- $ \sin(2\pi + x) = \sin(x) $
- $ \cos(2\pi + x) = \cos(x) $
- $ \tan(2\pi + x) = \tan(x) $
- $ \cot(2\pi + x) = \cot(x) $
2.3. Công thức nhân lượng giác
Công thức nhân đôi
- $\sin(2a) = 2\sin a \cos a.$
- $\cos(2a) = \cos^2 a – \sin^2 a = 2\cos^2 a – 1 = 1 – 2\sin^2 a.$
- $\tan(2a) = \frac{2\tan a}{1 – \tan^2 a} \quad (\text{với } \tan^2 a \neq 1).$
Công thức nhân ba
- $\sin 3x = 3\sin x – 4{\sin ^3}x$
- $\cos 3x = 4{\cos ^3}x – 3\cos x$
- $\tan 3x = \frac{{3\tan x – {{\tan }^3}x}}{{1 – 3{{\tan }^2}x}}$
Công thức nhân bốn
- $\sin 4x = 4\sin x.{\cos ^3}x – 4\cos x.{\sin ^3}x$
- $\cos 4x = 8{\cos ^4}x – 8{\cos ^2}x + 1$ $ = 8{\sin ^4}x – 8{\sin ^2}x + 1$
2.4. Công thức hạ bậc
Hạ bậc 2
- Hạ bậc của \(\sin^2 a\): $\sin^2 a = \frac{1 – \cos(2a)}{2}.$
- Hạ bậc của \(\cos^2 a\): $\cos^2 a = \frac{1 + \cos(2a)}{2}.$
- Hạ bậc của \(\tan^2 a\): $\tan^2 a = \frac{1 – \cos(2a)}{1 + \cos(2a)}.$
Hạ bậc 3
- Hạ bậc của ${\sin ^3}x$: ${\sin ^3}x = \frac{{3\sin x – \sin 3x}}{4}$
- Hạ bậc của ${\cos ^3}x$: ${\cos ^3}x = \frac{{3\cos x + \cos 3x}}{4}$
2.5. Công thức biến đổi tích thành tổng
- $\sin a \cos b = \frac{1}{2} [\sin(a + b) + \sin(a – b)].$
- $\cos a \cos b = \frac{1}{2} [\cos(a + b) + \cos(a – b)].$
- $\sin a \sin b = \frac{1}{2} [\cos(a – b) – \cos(a + b)].$
2.6. Công thức biến đổi tổng thành tích
Biến đổi tổng thành tích (dạng sin):
- $\sin A + \sin B = 2 \sin\left(\frac{A + B}{2}\right) \cos\left(\frac{A – B}{2}\right)$
- $\sin A – \sin B = 2 \cos\left(\frac{A + B}{2}\right) \sin\left(\frac{A – B}{2}\right)$
Biến đổi tổng thành tích (dạng cos):
- $\cos A + \cos B = 2 \cos\left(\frac{A + B}{2}\right) \cos\left(\frac{A – B}{2}\right)$
- $\cos A – \cos B = -2 \sin\left(\frac{A + B}{2}\right) \sin\left(\frac{A – B}{2}\right)$
- $\sin x + \cos x = \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right)$ $ = \sqrt 2 \cos \left( {x – \frac{\pi }{4}} \right)$
- $\sin x – \cos x = \sqrt 2 \sin \left( {x – \frac{\pi }{4}} \right)$ $ = – \sqrt 2 \cos \left( {x + \frac{\pi }{4}} \right)$
- ${\sin ^4}x + {\cos ^4}x = 1 – \frac{1}{2}{\sin ^2}\left( {2x} \right)$ $ = \frac{1}{4}\cos \left( {4x} \right) + \frac{3}{4}$
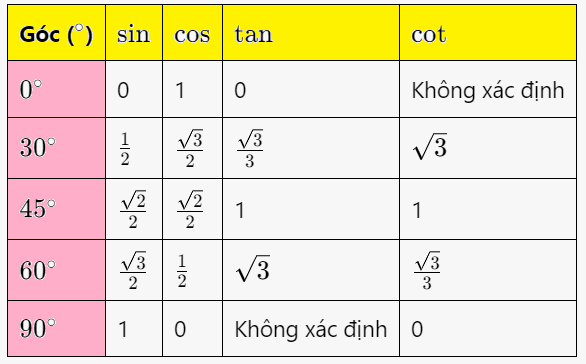
3. Bảng giá trị lượng giác của các góc đặc biệt
Bảng giá trị lượng giác thường dùng (0 ≤ α ≤ 900)
Các góc đặc biệt (\(0^\circ, 30^\circ, 45^\circ, 60^\circ, 90^\circ\)) thường được sử dụng trong bài toán lượng giác. Giá trị của các hàm lượng giác tại các góc này là:
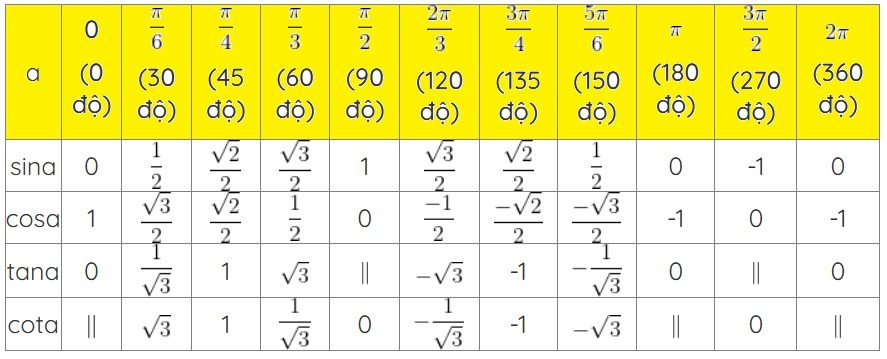
Bảng giá trị lượng giác thường dùng (0 ≤ α ≤ 3600)
4. Bài tập
Bài tập 1: Tính giá trị lượng giác \(\sin(45^\circ + 30^\circ)\).
Lời giải
Áp dụng công thức cộng:$\sin(a + b) = \sin a \cos b + \cos a \sin b.$
Thay \(a = 45^\circ\) và \(b = 30^\circ\):
$\sin(45^\circ + 30^\circ) = \sin 45^\circ \cos 30^\circ + \cos 45^\circ \sin 30^\circ.$
Sử dụng bảng giá trị lượng giác:
$\sin 45^\circ = \cos 45^\circ = \frac{\sqrt{2}}{2}, \quad \sin 30^\circ = \frac{1}{2}, \quad \cos 30^\circ = \frac{\sqrt{3}}{2}.$
Tính toán:$\sin(45^\circ + 30^\circ) = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{3}}{2} + \frac{\sqrt{2}}{2} \cdot \frac{1}{2} = \frac{\sqrt{6}}{4} + \frac{\sqrt{2}}{4} = \frac{\sqrt{6} + \sqrt{2}}{4}.$
Ví dụ 2: Giải phương trình \(\sin x = \frac{\sqrt{3}}{2}\) trên miền \(0^\circ \leq x \leq 360^\circ\).
Lời giải
Dựa vào bảng giá trị lượng giác:$\sin x = \frac{\sqrt{3}}{2} \iff x = 60^\circ \text{ hoặc } x = 180^\circ – 60^\circ = 120^\circ.$
Kết quả: $x = 60^\circ \text{ và } x = 120^\circ.$
Xem thêm:
Các công thức lượng giác là nền tảng quan trọng trong toán học và có nhiều ứng dụng thực tiễn. Việc thành thạo các công thức cơ bản như cộng, nhân đôi, hạ bậc, và chuyển đổi tích thành tổng không chỉ giúp bạn giải quyết nhanh chóng các bài toán lượng giác từ đơn giản đến phức tạp, mà còn mở ra khả năng áp dụng linh hoạt trong khoa học, kỹ thuật và cuộc sống hàng ngày.