Các hàm lượng giác như sin, cos, tan không chỉ là những khái niệm trừu tượng mà còn là công cụ thiết yếu, giúp con người giải quyết các bài toán từ đơn giản đến phức tạp trong thực tiễn. Việc tính toán chính xác giá trị lượng giác đóng vai trò then chốt, đòi hỏi sự hiểu biết sâu rộng và kỹ năng vững vàng. Hãy cùng khám phá các phương pháp tính giá trị lượng giác để tự tin chinh phục những thách thức toán học đầy thú vị!
Bài tập 1. Tính các giá trị lượng giác của góc \(\alpha = \frac{2017\pi}{3}\).
Lời giải
Ta có:
$\frac{{2017\pi }}{3} = \frac{\pi }{3} + 672\pi $
$ \Rightarrow \cos \left( {\frac{{2017\pi }}{3}} \right)$ $ = \cos \left( {\frac{\pi }{3} + 672\pi } \right) = \cos \frac{\pi }{3} = \frac{1}{2}$
$ \Rightarrow \sin \frac{{2017\pi }}{3} = \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2},\quad $
$\tan \frac{{2017\pi }}{3} = \sqrt 3 $
$\cot \frac{{2017\pi }}{3} = \frac{1}{{\sqrt 3 }}.$
Bài tập 2. Cho \(\tan(\pi + x) = 1 – \sqrt{2}\) với \(\frac{3\pi}{2} < \alpha < 2\pi\). Tính \(\cot\left(\frac{\pi}{2} + x\right)\).
Lời giải
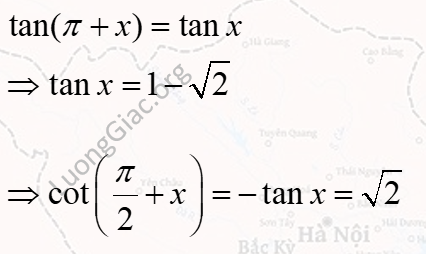
Bài tập 3. Cho \(\cos \alpha = \frac{1}{3}\). Tính \(\sin \left(\alpha – \frac{3\pi}{2} \right)\).
Lời giải
Ta có: $\sin \left( {\alpha – \frac{{3\pi }}{2}} \right)$ $ = \sin \left( {\alpha – 2\pi + \frac{\pi }{2}} \right)$ $ = \sin \left( {\alpha + \frac{\pi }{2}} \right)$ $ = \cos \alpha = \frac{1}{3}.$
Bài tập 4. Rút gọn biểu thức: $A = \cos(5\pi – x) – \sin \left(\frac{3\pi}{2} + x \right) + \tan \left(\frac{3\pi}{2} – x \right) + \cot(3\pi – x).$
Lời giải
Ta có $\cos(5\pi – x) = \cos(\pi – x + 2.2\pi) = \cos(\pi – x) = -\cos x;$
$\sin \left(\frac{3\pi}{2} + x \right) = -\sin \left(\pi + \frac{\pi}{2} + x \right) = -\cos x;$
$\tan \left(\frac{3\pi}{2} – x \right) = \tan \left(\pi + \frac{\pi}{2} – x \right) = \tan \left(\frac{\pi}{2} – x \right) = \cot x;$
$\cot(3\pi – x) = \cot(-x) = -\cot x;$
Suy ra $A = -\cos x – (-\cos x) + \cot x + (-\cot x) = 0.$
Bài tập 5. Rút gọn biểu thức $A = \cos \left(\frac{\pi}{2} + x \right) + \cos (2\pi – x) + \cos (3\pi + x).$
Lời giải
Ta có: $ \begin{cases} \cos \left(\frac{\pi}{2} + x \right) = -\sin x \\ \cos (2\pi – x) = \cos x \\ \cos (3\pi + x) = -\cos x \end{cases} $
$ \Rightarrow A = -\sin x + \cos x – \cos x = -\sin x. $
Bài tập 6. Rút gọn biểu thức $D = \cos(5\pi – x) – \sin \left(\frac{3\pi}{2} + x \right) + \tan \left(\frac{3\pi}{2} – x \right) + \cot(3\pi – x).$
Lời giải
Ta có $\cos(5\pi – x) = \cos(4\pi + \pi – x) = \cos(\pi – x) = -\cos x;$
$\sin \left(\frac{3\pi}{2} + x \right) = \sin \left(2\pi – \frac{\pi}{2} + x \right) = \sin \left(-\frac{\pi}{2} + x \right) = -\sin x;$
$\tan \left(\frac{3\pi}{2} – x \right) = \tan \left(\pi + \frac{\pi}{2} – x \right) = \tan \left(\frac{\pi}{2} – x \right) = \cot x;$
$\cot(3\pi – x) = \cot(-x) = -\cot x;$ $\Rightarrow D = -\cos x – \sin x.$
Bài tập 7. Cho tam giác \(ABC\), chứng minh rằng \(\sin(A + B + 2C) = -\sin C\).
Lời giải
Ta có \(A + B + C = 180^\circ\)
\(\Rightarrow A + B + 2C = 180^\circ + C\).
\(\Rightarrow \sin(A + B + 2C) = \sin(180^\circ + C) = -\sin C\).
Bài tập 8. Tính giá trị của biểu thức $B = \cos 20^\circ + \cos 40^\circ + \cos 60^\circ + \ldots + \cos 180^\circ.$
Lời giải
Ta có \(\cos(180^\circ – x) = -\cos x\)
\(\Rightarrow \cos x + \cos (180^\circ – x) = 0\).
$ \begin{cases} \cos 20^\circ + \cos 160^\circ = 0 \\ \cos 40^\circ + \cos 140^\circ = 0 \\ \cos 60^\circ + \cos 120^\circ = 0 \\ \cos 80^\circ + \cos 100^\circ = 0 \end{cases} $
\(\Rightarrow B = \cos 90^\circ + \cos 180^\circ = -1\).
Bài tập 9. Tính giá trị của biểu thức $ A = \sin \frac{7\pi}{6} + \cos 9\pi + \tan \left(-\frac{5\pi}{4}\right) + \cot \frac{7\pi}{2}. $
Lời giải
Ta có $ A = \sin \left(\pi + \frac{\pi}{6} \right) + \cos (\pi + 4.2\pi) – \tan \left(\pi + \frac{\pi}{4} \right) + \cot \left(\frac{\pi}{2} + 3\pi \right). $
$ = -\sin \frac{\pi}{6} + \cos \pi – \tan \frac{\pi}{4} + \cot \frac{\pi}{2}. $
$ = -\frac{1}{2} – 1 – 1 + 0 = -\frac{5}{2}. $
Bài tập 10. Với điều kiện có nghĩa, hãy rút gọn biểu thức sau $ B = \sqrt{2} – \frac{1}{\sin(x + 2013\pi)} \cdot \sqrt{\frac{1}{1 + \cos x} + \frac{1}{1 – \cos x}} $ với \(\pi < x < 2\pi\).
Lời giải
Ta có $ \sin(x + 2013\pi) = \sin(x + \pi + 1006.2\pi) = \sin(x + \pi) = -\sin x. $
Do đó $ B = \sqrt{2} + \frac{1}{\sin x} \cdot \sqrt{\frac{1 – \cos x + 1 + \cos x}{(1 – \cos x)(1 + \cos x)}}. $
$ = \sqrt{2} + \frac{1}{\sin x} \cdot \sqrt{\frac{2}{1 – \cos^2 x}}. $
$ = \sqrt{2} + \frac{1}{\sin x} \cdot \sqrt{\frac{2}{\sin^2 x}}. $
$ = \sqrt{2} \left( 1 + \frac{1}{\sin x |\sin x|} \right). $
Vì \(\pi < x < 2\pi\) nên \(\sin x < 0\), do đó $ B = \sqrt{2} \left( 1 – \frac{1}{\sin^2 x} \right) = -\sqrt{2} \cot^2 x. $
Sau khi hoàn thành các dạng bài tập tính giá trị lượng giác, bạn không chỉ rèn được kỹ năng tính toán mà còn củng cố toàn bộ kiến thức nền tảng về góc, cung và đường tròn lượng giác. Việc hiểu rõ bản chất của các giá trị $\sin$, $\cos$, $\tan$, $\cot$ sẽ giúp bạn giải quyết linh hoạt mọi bài toán lượng giác từ cơ bản đến nâng cao.
Nếu bạn chưa thực sự nắm vững phần lý thuyết, hãy xem lại bài Giá trị lượng giác của một góc, nơi trình bày đầy đủ các khái niệm và mối liên hệ giữa góc và các hàm lượng giác. Tiếp theo, để hiểu sâu hơn về quá trình tính toán, bạn có thể đọc Tính giá trị lượng giác của một cung — bài viết hướng dẫn chi tiết từng bước áp dụng công thức.
Trong quá trình làm bài, điều quan trọng là xác định dấu của các giá trị lượng giác trong 4 góc phần tư, tránh nhầm lẫn khi góc vượt quá $90°$ hoặc $180°$. Hãy đọc thêm Dấu của các giá trị lượng giác để nắm quy tắc dấu một cách chắc chắn.
Ngoài ra, với các bài tập có góc đặc biệt, việc ghi nhớ Bảng giá trị lượng giác đặc biệt (0°, 30°, 45°, 60°, 90°) sẽ giúp bạn rút ngắn thời gian tính toán và kiểm tra kết quả nhanh chóng.
Khi kết hợp thành thạo cả lý thuyết và bảng tra cứu, bạn sẽ làm chủ hoàn toàn mảng tính giá trị lượng giác, sẵn sàng bước vào các chuyên đề nâng cao hơn như phương trình và công thức lượng giác.