Công thức biến đổi lượng giác là chìa khóa vàng trong lượng giác. Từ biến tổng thành tích, tích thành tổng, chúng giúp bạn “hô biến” các biểu thức phức tạp thành đơn giản chỉ trong tích tắc. Hãy tưởng tượng: chỉ vài bước, bạn sẽ làm chủ những bài toán khó nhằn! Đọc tiếp để nắm giữ bí quyết chinh phục toán học đầy thú vị này nhé!
1. Công thức biến đổi lượng giác
Chúng ta có 2 nhóm công thức biến đổi là tích thành tổng và tổng thành tích. Cụ thể
1.1 Biến đổi tích thành tổng
Khi biến đổi một biểu thức lượng giác tích thành tổng thì bạn cần nhớ ngay tới 4 công thức sau:
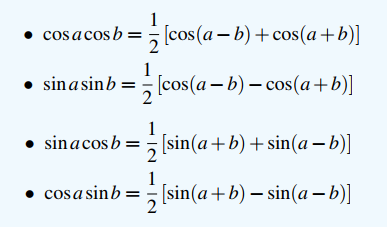
1.2 Biến đổi tổng thành tích
Và khi biến đổi biểu thức lượng giác tích tổng thành tích bạn cần nhớ ngay tới 6 công thức sau:
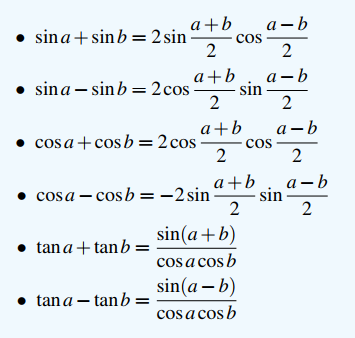
2. Bài tập vận dụng
Ví dụ 1: Biến đổi mỗi biểu thức sau đây thành một tổng:
a) \( A = 2 \sin(a+b) \sin(a-b) \)
b) \( B = \sin x \sin 2x \sin 3x \)
c) \( C = 8 \cos x \sin 2x \sin 3x \)
d) \( D = \cos x \cos(x + 60^\circ) \cos(x – 60^\circ) \)
Lời giải
a)
$A = 2\sin (a + b)\sin (a – b)$ $ = 2 \cdot \frac{1}{2}[\cos (a + b – a + b) – \cos (a + b + a – b)]$ $ = \cos 2b – \cos 2a.$
Vậy \( A = 2\sin(a+b)\sin(a-b) = \cos 2b – \cos 2a. \)
b)
$B = \sin x\sin 2x\sin 3x$ $ = \sin 3x(\sin 2x\sin x)$ $ = \frac{1}{2}\sin 3x[\cos x – \cos 3x]{\rm{ }}$ $ = \frac{1}{2}\sin 3x\cos x – \frac{1}{2}\sin 3x\cos 3x$ $ = \frac{1}{4}[\sin 2x + \sin 4x] – \frac{1}{4}\sin 6x$
Vậy $B = \sin x\sin 2x\sin 3x$ $ = \frac{1}{4}\sin 2x + \frac{1}{4}\sin 4x – \frac{1}{4}\sin 6x$
c)
\( C = 8\cos x \sin 2x \sin 3x = 8\sin 3x \sin 2x \cos x = 4 [\cos x – \cos 5x] \cos x \)
\( = 4\cos^2 x – 4\cos 5x \cos x = 2(1 + \cos 2x) – 2(\cos 4x + \cos 6x) \)
Vậy \( C = 8\cos x \sin 2x \sin 3x = 2 + 2\cos 2x – 2\cos 4x – 2\cos 6x \)
d)
$D = \cos x\cos (x + {60^0})\cos (x – {60^0})$ $ = \cos x \cdot \frac{1}{2}[\cos \left( {{\rm{12}}{{\rm{0}}^0}} \right) + \cos 2x]$ $ = \frac{1}{2}\cos x\left[ { – \frac{1}{2} + \cos 2x} \right]$ $ = – \frac{1}{4}\cos x + \frac{1}{2}\cos 2x\cos x{\rm{ }}$ $ = – \frac{1}{4}\cos x + \frac{1}{4}\cos 2x + \frac{1}{4}\cos 4x$
Vậy $D = \cos x\cos (x + {60^0})\cos (x – {60^0})$ $ = – \frac{1}{4}\cos x + \frac{1}{4}\cos 2x + \frac{1}{4}\cos 4x.$
Ví dụ 2. Biến đổi các biểu thức sau đây thành một tích:
a) \( A = \sin a + \sin 3a + \sin 5a \)
b) \( B = 1 + \cos x + \cos 2x + \cos 3x \)
Lời giải
a)
$\sin a + \sin 3a + \sin 5a$ $ = \sin 5a + \sin a + \sin 3a$ $ = 2\sin 3a\cos 2a + \sin 3a$ $ = \sin 3a(2\cos 2a + 1).$
Vậy \( A = \sin a + \sin 3a + \sin 5a = \sin 3a (2\cos 2a + 1). \)
b)
\( B = 1 + \cos x + \cos 2x + \cos 3x = (\cos 3x + \cos x) + (\cos 2x + 1) \)
$ = 2\cos 2x\cos x + 2{\cos ^2}x – 1 + 1$ $ = 2\cos x(\cos 2x + \cos x)$ $ = 2\cos x \cdot 2\cos \frac{{3x}}{2}\cos \frac{x}{2}$
Vậy $B = 1 + \cos x + \cos 2x + \cos 3x$ $ = 4\cos x\cos \frac{{3x}}{2}\cos \frac{x}{2}$
Bài tập 3. Rút gọn biểu thức lượng giác sau
a) \( 4\sin 2a \sin 4a \sin 6a \)
b) \( \sin \left( x + \frac{\pi}{6} \right) \sin \left( x – \frac{\pi}{6} \right) \cos 2x \)
Lời giải
a) Ta có 4sin2asin4asin6a = sin4a + sin8a − sin12a
b) Ta có \( \sin \left( x + \frac{\pi}{6} \right) \sin \left( x – \frac{\pi}{6} \right) \cos 2x \)
$ = \frac{1}{2} \left[ \cos \frac{\pi}{3} – \cos 2x \right] \cos 2x $ $ = \frac{1}{2} \cos \frac{\pi}{3} – \frac{1}{2} \cos^2 2x $ $ = \frac{1}{4} – \frac{1}{2} \cdot \frac{1 + \cos 4x}{2} $ $ = -\frac{\cos 4x}{4}. $
Hãy nhớ vững các công thức biến đổi lượng giác cơ bản như công thức tổng và hiệu, công thức nhân đôi. Đây là những “người bạn đồng hành” đắc lực giúp bạn giải quyết các bài toán phức tạp một cách nhanh chóng và hiệu quả. Đừng quên luyện tập thường xuyên để thành thạo cách áp dụng chúng vào giải phương trình, chứng minh bất đẳng thức hay các bài toán thực tế. Sự hiểu biết và linh hoạt trong việc sử dụng các công thức này sẽ là nền tảng quan trọng giúp bạn tự tin hơn khi học các công thức lượng giác tiếp theo.
