Nhận dạng một tam giác là một dạng bài tập quan trọng trong hình học lượng giác, giúp xác định loại tam giác dựa trên các yếu tố như góc, cạnh và các biểu thức lượng giác. Thông qua các đẳng thức và bất đẳng thức về sin, cos, tan, dạng bài này cho phép kiểm tra xem một tam giác có phải là tam giác vuông, đều, cân hay bất kỳ loại nào khác. Ngoài ra, nó còn giúp nhận biết tam giác dựa trên các tính chất đặc biệt như định lý cosin, định lý sin hay các công thức biến đổi lượng giác. Đây là một chủ đề quan trọng, thường xuất hiện trong các bài kiểm tra và kỳ thi toán học.
1. Lý thuyết nhận dạng tam giác

2. Bài tập
Bài tập 1. Chứng minh rằng DABC vuông khi sinAsinC = cosAcosC.
Lời giải
Ta có $\sin A\sin C = \cos A\cos C$
$ \Leftrightarrow \cos A\cos C – \sin A\sin C = 0$
$ \Leftrightarrow \cos (A + C) = 0$
$ \Leftrightarrow – \cos B = 0$
$ \Leftrightarrow \cos B = 0 \Leftrightarrow B = {90^0}$
Bài tập 2. Chứng minh rằng DABC cân khi 2sinAsinB = 1 + cosC. (1)
Lời giải
Ta có (1) tương đương với
$ \cos(A – B) – \cos(A + B) = 1 + \cos C $
$ \Leftrightarrow \cos(A – B) + \cos C = 1 + \cos C $
$ \Leftrightarrow \cos(A – B) = 1 \Leftrightarrow A – B = 0 \Leftrightarrow A = B. $
Vậy tam giác ABC cân tại C
Bài tập 3. Cho tam giác ABC với diện tích S và R là bán kính đường tròn ngoại tiếp. Chứng minh rằng:
$\sin 2A + \sin 2B + \sin 2C = \frac{2S}{R^2}.$
Lời giải
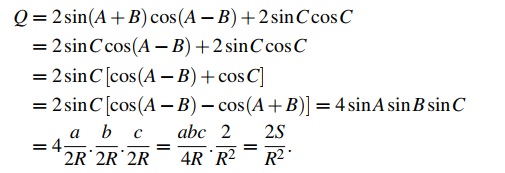
Nhận dạng tam giác.
Bài tập 4. Cho tam giác ABC. Chứng minh rằng asin(B − C) + bsin(C − A) + csin(A − B) = 0
Lời giải
Đẳng thức cần chứng minh tương đương với:
2R[sinAsin(B – C) + sinBsin(C – A) + sinCsin(A – B)] = 0
Mà ta có
- sinAsin(B – C) = sin(B + C)sin(B – C) = – (cos2B – cos2C)
- sinBsin(C – A) = sin(C + A)sin(C – A) = – (cos2C – cos2A)
- sinCsin(A – B) = sin(A + B)sin(A – B) = – (cos2A – cos2B)
Cộng lại ta được: sinAsin(B – C) + sinBsin(C – A) + sinCsin(A – B) = 0:
Từ đây ta có điều phải chứng minh.
Bài tập 5. Cho tam giác ABC. Chứng minh rằng:
\[\frac{a + b}{a – b} \cdot \tan \frac{A – B}{2} = \tan \frac{A + B}{2}.\]
Lời giải
\[\frac{a + b}{a – b} \cdot \tan \frac{A – B}{2} = \frac{2R (\sin A + \sin B)}{2R (\sin A – \sin B)} \cdot \tan \frac{A – B}{2}\]
\[= \frac{2 \sin \frac{A + B}{2} \cos \frac{A – B}{2}}{2 \cos \frac{A + B}{2} \sin \frac{A – B}{2}} \cdot \frac{\sin \frac{A – B}{2}}{\cos \frac{A – B}{2}} = \tan \frac{A + B}{2}.\]
Từ đây ta có điều phải chứng minh.
Bài tập 6. Cho A; B; C và a, b, c là các góc và các cạnh của tam giác ABC. Chứng minh rằng:
\[\frac{2 \sin (A – B)}{\sin C} = \frac{a^2 – b^2}{c^2}.\]
Lời giải
\[\frac{a^2 – b^2}{c^2} = \frac{4R^2 (\sin^2 A – \sin^2 B)}{4R^2 \sin^2 C} = \frac{1 – \cos 2A – (1 – \cos 2B)}{\sin^2 C}\]
\[= \frac{\cos 2B – \cos 2A}{\sin^2 C} = \frac{-2 \sin (B + A) \sin (B – A)}{\sin^2 C}\]
\[= \frac{2 \sin C \sin (A – B)}{\sin^2 C} = \frac{2 \sin (A – B)}{\sin C}.\]
Từ đây ta có điều phải chứng minh.
Bài tập 7. Chứng minh rằng với mọi tam giác nhọn ABC ta luôn có: \[ \frac{\sin A + \sin B – \sin C}{\cos A + \cos B – \cos C + 1} = \tan \frac{A}{2} \tan \frac{B}{2} \cot \frac{C}{2}. \]
Lời giải
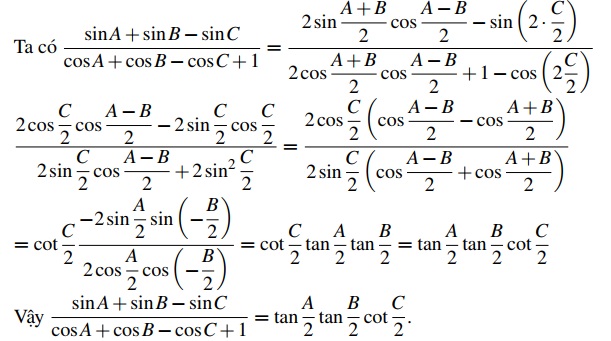
Bài tập 8. Cho A; B; C là 3 đỉnh của một tam giác. Chứng minh rằng
\[ \text{a) } \sin A + \sin B + \sin C = 4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2} \]
\[ \text{b) } \cos A + \cos B + \cos C = 1 + 4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \]
\[ \text{c) } \sin 2A + \sin 2B + \sin 2C = 4 \sin A \sin B \sin C \]
\[ \text{d) } \cos 2A + \cos 2B + \cos 2C + 1 = -4 \cos A \cos B \cos C \]
\[ \text{e) } \sin^2 A + \sin^2 B + \sin^2 C = 2 + 2 \cos A \cos B \cos C \]
\[ \text{f) } \cos^2 A + \cos^2 B + \cos^2 C = 1 – 2 \cos A \cos B \cos C \]
\[ \text{g) } \tan A + \tan B + \tan C = \tan A \tan B \tan C \]
\[ \text{h) } \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{B}{2} \tan \frac{C}{2} + \tan \frac{C}{2} \tan \frac{A}{2} = 1 \]
Lời giải


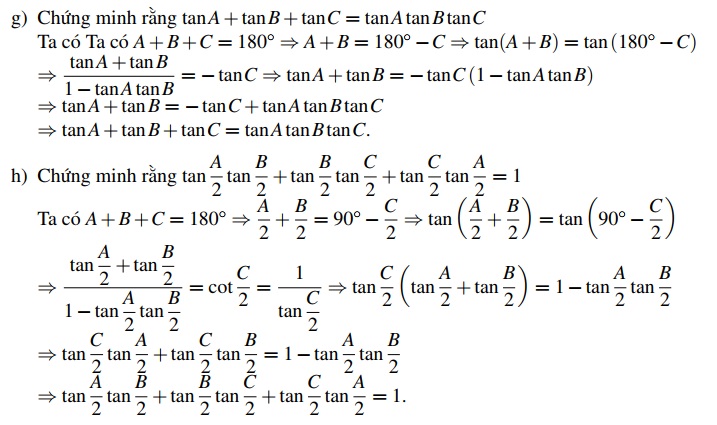
Dạng bài nhận dạng một tam giác không chỉ giúp rèn luyện kỹ năng biến đổi lượng giác mà còn củng cố hiểu biết về các tính chất hình học quan trọng. Vì vậy, việc luyện tập thường xuyên sẽ giúp nâng cao tư duy toán học và khả năng vận dụng linh hoạt các công thức.