Dạng toán hàm số lượng giác là một trong những nội dung trọng tâm và cũng “khó nhằn” nhất của chương trình Toán 11, thường xuyên xuất hiện trong các bài kiểm tra, thi học kỳ và đề thi đánh giá năng lực. Để giúp học sinh nắm vững bản chất, nhận diện nhanh từng dạng bài và tránh những lỗi sai thường gặp, bài viết “Các dạng Toán Bài Hàm Số Lượng Giác Toán 11 – Giải Chi Tiết” sẽ hệ thống đầy đủ các dạng toán quan trọng, kèm theo phương pháp giải rõ ràng, lập luận chặt chẽ và ví dụ minh họa cụ thể. Qua đó, học sinh không chỉ học cách giải bài mà còn hiểu sâu bản chất, nâng cao tư duy và tự tin chinh phục các bài toán từ cơ bản đến nâng cao.
Bài tập 1: Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hoá bởi hàm số $h\left( t \right)=90\text{cos}\left( \frac{\pi }{10}t \right)$, trong đó $h\left( t \right)$ là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm $t$ giây.
a) Tìm chu kì của sóng.
b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
Lời giải
a) Chu kì của sóng là $T=\frac{2\pi }{\frac{\pi }{10}}=20$ (giây).
b) Chiều cao của sóng tức là chiều cao của nước đạt được trong một chu kì dao động.
Ta có: $h\left( 20 \right)=90\text{cos}\left( \frac{\pi }{10}\cdot 20 \right)=90\left( \text{ }\!\!~\!\!\text{ cm} \right)$.
Vậy chiều cao của sóng là 90 cm.
Bài tập 2: Chiều cao so với mực nước biển trung bình tại thời điểm ${t}$ (giây) của mỗi cơn sóng được cho bởi hàm số $h\left( t \right)=75\sin \left( \frac{\pi t}{8} \right)$, trong đó $h\left( t \right)$ được tính bằng centimét.

a) Chiều cao của sóng tại các thời điểm 5 giây bằng $69,3$cm.
b) Chiều cao của sóng tại các thời điểm 20 giây bằng $75$cm
c) Trong 30 giây đầu tiên (kể từ mốc ${t=0}$ giây), thời điểm để sóng đạt chiều cao lớn nhất 6 giây
d) Trong 30 giây đầu tiên (kể từ mốc ${t=0}$ giây), thời điểm để sóng đạt chiều cao lớn nhất 18 giây (Tất cả kết quả được làm tròn đến hàng phần mười)
Lời giải
a) Đúng: Khi ${t=5}$ ta có: $h\left( 5 \right)=75\sin \left( \frac{\pi .5}{8} \right)\approx 69,3$cm.
b) Đúng: Khi ${t=20}$ ta có: $h\left( 20 \right)=75\sin \left( \frac{\pi .20}{8} \right)=75$cm.
c) Sai:
d) Sai: Ta có: ${\sin \left(\frac{\pi t}{8}\right) \leq 1 \Rightarrow 75 \sin \left(\frac{\pi t}{8}\right) \leq 75}$ hay $h\left( t \right)\le 75$.
Giá trị lớn nhất của $h\left( t \right)$ là 75 khi đó ${\sin \left(\frac{\pi t}{8}\right)=1 \Rightarrow \frac{\pi t}{8}=\frac{\pi}{2}+k 2 \pi(k \in \mathbb{Z})}$ ${\sin \left(\frac{\pi t}{8}\right)=1 \Rightarrow \frac{\pi t}{8}=\frac{\pi}{2}+k 2 \pi(k \in \mathbb{Z})}$. Vì ${t \in[0 ; 30] \Rightarrow t \in\{4 ; 20\}}$ (ứng với ${k}$ bằng 0 và 1).
Vậy tại các thời điểm 4 giây hoặc 20 giây (trong 30 giây đầu tiên) thì cơn sóng đạt chiều cao cực đại là$75~$cm.
Bài tập 3: Một cái guồng nước có vành kim loại ngoài cùng là một đường tròn tâm $O$, bán kính là $4~m$. Xét chất điểm $M$ thuộc đường tròn đó và góc $\alpha =\left( OA,OM \right)$. Giả sử mực nước lúc đang xét là tiếp xúc với đường tròn $\left( O\,;\,4 \right)$và guồng nước quay theo chiều dương (ngược chiều kim đồng hồ). Biết rằng guồng nước quay hết một vòng sau 40 giây $(t=0$ giây khi điểm $M$ trùng $A$). Hỏi thời điểm nào (trong 1 vòng quay đầu tiên) thì điểm $M$ ở vị trí cao nhất so với mặt nước?
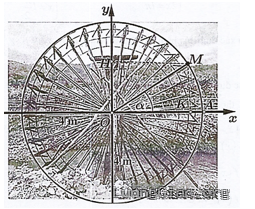
Lời giải
Ta có: $h\left( x \right)=4+4\sin \alpha $.
Khi $M$ ở vị trí cao nhất so với mặt nước tức là $h\left( x \right)=8$ thì $\sin \alpha =1\Rightarrow \alpha =\frac{\pi }{2}$ (vì chỉ xét 1 vòng quay đầu tiên). Thời gian thực hiện của guồng nước là: $t=\frac{\frac{\pi }{2}\cdot 40}{2\pi }=10$ (giây).
Bài tập 4: Một con lắc lò xo dao động điều hoà quanh vị trí cân bằng theo phương trình $y=25\text{sin}4\pi t$ ở đó $y$ được được tính bằng centimét còn thời gian $t$ được tính bằng giây. Gọi $a$ là chu kì dao động của con lắc lò xo; $b$(Hz) là tần số dao động của con lắc, tức là số lần dao động trong một giây và $c$ (cm) là khoảng cách giữa điểm cao nhất và thấp nhất của con lắc. Tính $a+b+c$
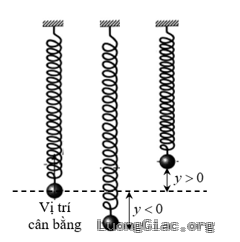
Lời giải
Hàm số $y=25\text{sin}4\pi t$ tuần hoàn với chu kì $T=\frac{2\pi }{4\pi }=\frac{1}{2}$ suy ra chu kì dao động của con lắc lò xo (tức là khoảng thời gian để con lắc thực hiện được một dao động toàn phần) là $T=\frac{1}{2}$ giây nên $a=0,5$.
Vì chu kì dao động của con lắc là $T=\frac{1}{2}$ giây nên trong 1 giây con lắc thực hiện được 2 dao động, tức là tần số dao động của con lắc là $b=f=\frac{1}{T}=2\text{ }\!\!~\!\!\text{ Hz}$.
Vì phương trình dao động của con lắc là $y=25\text{sin}4\pi t$ nên biên độ dao động của nó là $A=25\text{ }\!\!~\!\!\text{ cm}$
Từ đó khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc là $c=2A=50\text{ }\!\!~\!\!\text{ cm}$.
Vậy $a+b+c=0,5+2+50=52,5$.
Bài tập 5: Khi đu quay hoạt động, vận tốc theo phương ngang của một cabin $M$ phụ thuộc vào góc lượng giác $\alpha =\left( Ox,OM \right)$ theo hàm số ${{v}_{x}}=0,3\text{sin}\alpha \left( \text{m}/\text{s} \right)$.

a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của ${{v}_{{{x}^{\text{*}}}}}$
b) Dựa vào đồ thị của hàm số $\sin $, hãy cho biết trong vòng quay đầu tiên $\left( 0\le \alpha \le 2\pi \right)$, góc $\alpha $ ở trong các khoảng nào thì ${{v}_{x}}$ tăng.
Lời giải
a) Do $-1\le \text{sin}\alpha \le 1$ nên $-0,3\le \text{sin}\alpha \le 0,3$
Vậy giá trị lớn nhất của ${{v}_{x}}$ là $0,3\left( \text{ }\!\!~\!\!\text{ m} \right)$ và giá trị nhỏ nhất của ${{v}_{x}}$ là $-0,3\left( \text{ }\!\!~\!\!\text{ m} \right)$.
b) Dựa vào đồ thị hàm số $\sin $, ta thấy vòng quay đầu tiên $\left( 0\le \alpha \le 2\alpha \right)$; ${{v}_{x}}$ tăng khi $\pi \le \alpha \le 2\pi $
Skip to PDF content