Max – min của hàm số lượng giác

Phương pháp: Ta thường sử dụng ba cách làm sau đây

Sử dụng các bất đẳng thức cơ bản:

$\centerdot \,\,\,-1\le \sin x\le 1,\,\forall x\in \mathbb{R}$

$\centerdot \,\,\,-1\le \text{cos}\,x\le 1,\,\forall x\in \mathbb{R}$

$\centerdot \,\,\,0\le {{\sin }^{2}}x.\text{co}{{\text{s}}^{2}}x\le 1,\,\forall x\in \mathbb{R}$

$\centerdot \,\,\,0\le \left| \sin x \right|.\left| \text{cos}x \right|\le 1,\,\forall x\in \mathbb{R}$

Sử dụng điều diện có nghiệm

• $\centerdot \,\,\,\sin x=f\left( m \right)$ có nghiệm khi $-1\le f\left( m \right)\le 1$
• $\centerdot \,\,\,\text{cos}\,x=f\left( m \right)$ có nghiệm khi $-1\le f\left( m \right)\le 1$
• $\centerdot \,\,a\,\sin x+b\,\text{cos}\,x=c$ có nghiệm khi ${{a}^{2}}+{{b}^{2}}\ge {{c}^{2}}$

Sử dụng bảng biến thiên: Lập bảng biến thiên của hàm số từ đó đưa ra kết luận.

Bài tập 1: Trong hình dưới đây, một chiếc máy bay $A$ bay ờ độ cao $500\text{ }\!\!~\!\!\text{ m}$ theo một đường thẳng đi ngang qua phía trên trạm quan sát $T$ ở mặt đất. Hình chiếu vuông góc của $A$ lên mặt đất là $H$ và $\alpha $ là góc lượng giác $\left( Tx,TA \right)\left( 0<\alpha <\pi \right)$.

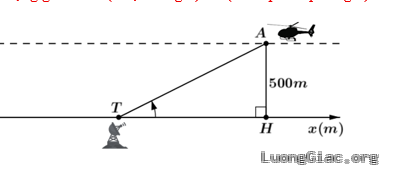
Hãy cho biết với $\frac{\pi }{6}<\alpha <\frac{2\pi }{3}$ thì ${{x}_{H}}$ nằm trong khoảng nào. Làm tròn kết quả đến hàng phần mười.

Lời giải

a) ${{x}_{H}}=500.\text{cot}\alpha $

b) Với $\frac{\pi }{6}<\alpha <\frac{2\pi }{3}$ thì $\frac{-\sqrt{3}}{3}<\text{cot}\alpha <\sqrt{3}$. Vậy ${{x}_{H}}\in \left\{ -288,7;866 \right\}$.

Bài tập 2: Giá trị nhỏ nhất của hàm số $y={{\sin }^{2}}x-4\sin x+2$

A. $-20$.

B. $0$.

C. $9$.

D. $-1$.

Lời giải

Ta có: $y = {\sin ^2}x – 4\sin x + 2$ $ = {\sin ^2}x – 4\sin x + 4 – 4 + 2$ $ = {\left( {\sin x – 2} \right)^2} – 2$

Do $\,\sin x\,\, \le 1\,$ $\, \Rightarrow {\left( {\sin x – 2} \right)^2} \le {( – 1)^2}$ $ \Rightarrow {\left( {\sin x – 2} \right)^2} – 2 \le – 1$

.

Bài tập 3: Cho hàm số $y=3-\sin \left( 2x+\frac{\pi }{4} \right)$. Xét tính đúng sai của các khẳng định sau:

a) Hàm số có tập xác định $D=\mathbb{R}$.

b) Giá trị nhỏ nhất của hàm số bằng 2

c) Giá trị lớn nhất của hàm số bằng 4

d) Tập giá trị của hàm số là $T=[2;4]$

Lời giải

a) Đúng: Ta có: hàm số có tập xác định $D=\mathbb{R}$.

b) Đúng: $ – 1 \le \sin \left( {2x + \frac{\pi }{4}} \right) \le 1$ $ \Leftrightarrow 1 \ge – \sin \left( {2x + \frac{\pi }{4}} \right) \ge – 1$ $ \Leftrightarrow 4 \ge 3 – \sin \left( {2x + \frac{\pi }{4}} \right) \ge 2$ $ \Leftrightarrow 4 \ge y \ge 2$

Giá trị nhỏ nhất của hàm số bằng 2

c) Đúng: Giá trị lớn nhất của hàm số bằng 4

d) Đúng: Vậy giá trị của hàm số là $T=[2;4]$.

Bài tập 4: Với giá trị nào của $m$ thì hàm số $y=\sin 3x-\cos 3x+m$ có giá trị lớn nhất bằng $\sqrt{2}.$

Lời giải

Ta có: $y = \sin 3x – \cos 3x + m$ $ = \sqrt 2 .\left( {\frac{1}{{\sqrt 2 }}\sin 3x – \frac{1}{{\sqrt 2 }}{\rm{cos3}}x} \right) + m$ $ = \sqrt 2 \sin \left( {3x – \frac{\pi }{4}} \right) + m \le \sqrt 2 + m$

Do đó giá trị lớn nhất của $y$bằng $\sqrt{2}$ khi $\sqrt{2}+m=\sqrt{2}\Leftrightarrow m=0.$

Bài tập 5: Số giờ có ánh sáng mặt trời của một thành phố X ở vĩ độ ${{40}^{0}}$ bắc trong ngày thứ $t$ của một năm không nhuận được cho bởi hàm số $d\left( t \right)=3\sin \left[ \frac{\pi }{182}\left( t-80 \right) \right]+12$, $t\in \mathbb{Z}$, $0<t\le 365$. Vào ngày nào trong năm thì thành phố X có ít giờ có ánh sáng mặt trời nhất?

Lời giải

Ta có: $\sin \left[ \frac{\pi }{182}\left( t-80 \right) \right]\ge -1$ $\forall t$ $\Rightarrow d\left( t \right)\ge 3.\left( -1 \right)+12=9$. Dấu $”=”$ xảy ra khi:

$\sin \left[ \frac{\pi }{182}\left( t-80 \right) \right]=-1$ $ \Leftrightarrow \frac{\pi }{{182}}\left( {t – 80} \right) = – \frac{\pi }{2} + k2\pi $ $ \Leftrightarrow t – 80 = – 91 + 364k$ $ \Leftrightarrow t = – 11 + 364k$

Mà $0<t\le 365$ $\Rightarrow 0<-11+364k\le 365\Leftrightarrow \frac{11}{364}<k\le \frac{376}{364}\Leftrightarrow k=1\left( k\in \mathbb{Z} \right)$$\Rightarrow t=353$.

Vậy thành phố X có ít giờ có ánh sáng mặt trời nhất vào ngày 353 trong năm.

Skip to PDF content

TẢI FILE PDF