Đổi đơn vị giữa độ và rađian, độ dài cung tròn là nội dung cơ bản nhưng rất quan trọng trong chương Lượng giác – Toán 11, giúp học sinh sử dụng chính xác công thức và tránh sai sót khi làm bài. Dạng toán này thường xuất hiện xuyên suốt các bài tập và đề kiểm tra, đặc biệt khi liên quan đến góc lượng giác và chuyển động tròn.
Để biểu diễn cung lượng giác có số đo trên đường tròn lượng giác ta thực hiện như sau:
- Chọn điểm $A\left( 1;0 \right)$ làm điểm đầu của cung.
- Xác định điểm cuối $M$ của cung sao cho $\overset\frown{AM}=\alpha $
Lưu ý:
- Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của $2\pi $ là: $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=\alpha +k2\pi ;k\in \mathbb{Z}$
- Ngoài ra, ta cũng có thể viết số đo bằng độ: $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=x{}^\circ +k360{}^\circ ,k\in \mathbb{Z}$
- Nếu ta có $\overset\frown{AM}=\alpha +k\frac{2\pi }{n};k,n\in \mathbb{Z}$ thì sẽ có $n$ điểm ngọn.
Hệ thức Chasles: Với ba tia $Ou,\,Ov,\,Ow$ bất kì thì ta có:
- $sd\left( Ou,\,Ov \right)+sd\left( Ov,\,Ow \right)=sd\left( Ou,\,Ow \right)+k{{.360}^{0\,}}\,\,\,\,\,\left( k\in \mathbb{Z} \right)$
- Từ đó ta có thể suy ra: $sd\left( Ou,\,Ov \right)=sd\left( Ou,\,Ow \right)-sd\left( Ov,\,Ow \right)+k{{.360}^{0\,}}\,\,\,\,\,\left( k\in \mathbb{Z} \right)$
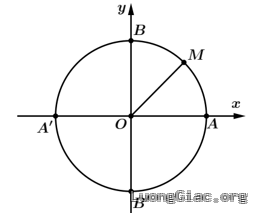
Bài tập 1: Biểu diễn trên đường tròn lượng giác điểm ngọn của cung lượng giác có số đo là $\frac{25\pi }{4}$
Lời giải
Ta có: $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=\frac{25\pi }{4}=\frac{\pi }{4}+\frac{24\pi }{4}=\frac{\pi }{4}+6\pi =\frac{\pi }{4}+2.3.\pi $
Vậy điểm cuối $M$ của cung $\overset\frown{AM}$ sẽ trùng với điểm ngọn của cung $\frac{\pi }{4}$. Suy ra $M$ là điểm chính giữa của cung nhỏ $\overset\frown{AB}$.
Bài tập 2:Biểu diễn trên đường tròn lượng giác các điểm ngọn của cung lượng giác có số đo là $-1485{}^\circ $
Lời giải
Ta có $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AB}=-1485{}^\circ =-45{}^\circ +\left( -4 \right).360{}^\circ $
Vậy điểm cuối $M$ của cung $\overset\frown{AB}$ sẽ trùng với điểm ngọn của cung $-45{}^\circ $.
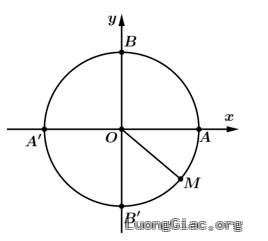
Suy ra $M$ là điểm chính giữa của cung nhỏ $\overset\frown{A{B}’}$.
Bài tập 3: Biểu diễn trên đường tròn lượng giác các điểm ngọn của cung lượng giác có số đo là: $\frac{\pi }{6}+k\frac{\pi }{2};k\in \mathbb{Z}$
Lời giải
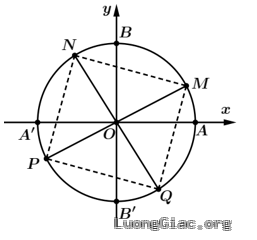
Ta có $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=\frac{\pi }{6}+k\frac{2\pi }{4}$ nên có 4 điểm ngọn trên đường tròn lượng giác.
Với $k=0\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=\frac{\pi }{6}$ có điểm ngọn là $M$
Với $k=1\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AN}=\frac{\pi }{6}+\frac{\pi }{2}$ có điểm ngọn là $N$
Với $k=2\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AP}=\frac{\pi }{6}+\pi $ có điểm ngọn là $P$
Với $k=3\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AQ}=\frac{\pi }{6}+\frac{3\pi }{2}$ có điểm ngọn là $Q$
Với $k=4\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AR}=\frac{\pi }{6}+2\pi $ có điểm ngọn là $R$. Lúc này điểm ngọn $R$ trùng với $M$
Vậy bốn điểm $M,N,P,Q$ tạo thành một hình vuông nội tiếp đường tròn lượng giác
Bài tập 4: Biểu diễn trên đường tròn lượng giác các điểm ngọn của cung lượng giác có số đo là $k\frac{\pi }{3};k\in \mathbb{Z}$
Lời giải
Ta có $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=k\frac{2\pi }{6}$ nên có 6 điểm ngọn trên đường tròn lượng giác.
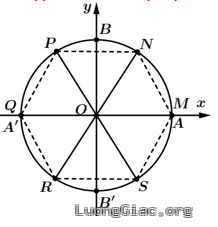
Với $k=0\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=0$ có điểm ngọn là $M$
Với $k=1\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AN}=\frac{\pi }{3}$ có điểm ngọn là $N$
Với $k=2\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AP}=\frac{2\pi }{3}$ có điểm ngọn là $P$
Với $k=3\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AQ}=\pi $ có điểm ngọn là $Q$
Với $k=4\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AR}=\frac{4\pi }{3}$ có điểm ngọn là $R$
Với $k=5\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AS}=\frac{5\pi }{3}$ có điểm ngọn là $S$
Với $k=6\Rightarrow \text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AT}=2\pi $ có điểm ngọn là $T$
Lúc này điểm ngọn $T$ trùng với $M$. Vậy sáu điểm $M;N;P;Q;R;S$ tạo thành một lục giác đều nội tiếp đường tròn lượng giác.
Bài tập 5: Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây.
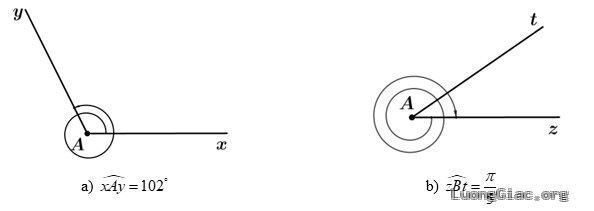
Lời giải
Số đo của góc lượng giác ${(A x, A y)}$ trong hình a) bằng: ${102^{\circ}+360^{\circ}=462^{\circ}}$.
Số đo của góc lượng giác ${(B t, B z)}$ trong hình b) bằng ${-\frac{\pi}{5}-2.2 \pi=-\frac{21 \pi}{5}}$.
Skip to PDF contentTẢI FILE PDF