Trong lượng giác, độ dài cung lượng giác là một khái niệm quan trọng giúp bạn kết nối trực tiếp giữa góc lượng giác và độ dài thực tế trên đường tròn. Mỗi góc khi quay trên đường tròn lượng giác đều tạo ra một cung, và độ dài cung này chính là đại lượng hình học biểu diễn “khoảng quay” của góc đó.
👉 Nếu bạn chưa nắm chắc khái niệm góc trong lượng giác, hãy xem lại bài Góc lượng giác để hiểu rõ cách xác định góc dương, góc âm và hướng quay trên trục tọa độ.
Một điểm cần lưu ý là công thức tính độ dài cung luôn sử dụng đơn vị radian thay vì độ. Điều này giúp các phép biến đổi và tính toán trở nên chính xác và thống nhất trong toàn bộ hệ thống lượng giác.
Nếu bạn đang quen với đơn vị độ (°), hãy tham khảo hướng dẫn Chuyển đổi giữa độ và radian trong lượng giác để áp dụng công thức đúng cách và tránh sai sót khi làm bài tập.
I. Lý thuyết độ dài cung lượng giác
Độ dài cung lượng giác là độ dài của một cung tròn được tạo ra bởi một góc trên đường tròn. Để biểu diễn rõ hơn, nó liên quan đến một khái niệm cơ bản trong hình học và lượng giác, và thường được tính dựa trên bán kính của đường tròn và góc mà cung đó mở ra.
Cung tròn bán kính \( R \) có số đo \( \alpha \) (\( 0 \leq \alpha \leq 2\pi \)), có số đo \( a^\circ \) (\( 0 \leq a \leq 360 \)) và có độ dài là \( l \) thì: $l = R\alpha = \frac{\pi a}{180} \cdot R \text{ do đó } \frac{\alpha}{\pi} = \frac{a}{180}$
Đặc biệt:
- \( 1 \) rad = \( \left( \frac{180}{\pi} \right)^\circ \),
- \( 1^\circ = \frac{\pi}{180} \) rad.
II. Bài tập
Bài tập 1. Một đường tròn có bán kính 36 m. Tìm độ dài của cung trên đường tròn đó có số đo là
a) \( \frac{3\pi}{4} \)
b) \( 51^\circ \)
c) \( \frac{1}{3} \)
Lời giải
Theo công thức tính độ dài cung tròn ta có \( l = R\alpha = \frac{\pi a}{180} \cdot R \) nên
a) Ta có \( l = R\alpha = 36 \cdot \frac{3\pi}{4} = 27\pi \approx 84,8m \)
b) Ta có \( l = \frac{\pi 51}{180} \cdot 36 = \frac{51\pi}{5} \approx 32,04 m. \)
c) Ta có \( l = R\alpha = 36 \cdot \frac{1}{3} = 12 \) m.
Bài tập 2. Cho đường tròn có đường kính \( R = 20 \) cm. Hãy tính độ dài cung tròn có số đo: \( \frac{\pi}{15} \); \( 1,5 \); \( 37^\circ \).
Lời giải
– \( l = \frac{\pi}{15} \cdot 20 \approx 4,19 \) cm.
– \( l = 1,5 \cdot 20 = 30 \) cm.
– \( l = \frac{37 \cdot \pi}{180} \cdot 20 \approx 12,91 \) cm.
Bài tập 3. Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây.
a) Tính góc (theo độ và radian) mà bánh xe quay được trong 1 giây.
b) Tính quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính bánh xe đạp là 680 mm.
Lời giải
a) Trong 1 giây, bánh xe quay được \( \frac{11}{5} \) vòng, tức là quay được một góc \( \frac{22\pi}{5} \) (rad) hay \( 792^\circ \).
b) Trong 1 phút, bánh xe lăn được \( l = 340 \cdot \frac{22\pi}{5} \cdot 60 \approx 281,990 \) (mm) \( \approx 282 \) m.
Bài tập . Trên đường tròn lượng giác gốc \( A \). Cho điểm \( M, N \) sao cho \( \text{sđ} \widehat{AM} = \frac{\pi}{5} \), \( \text{sđ} \widehat{AN} = -\frac{\pi}{5} \). Các điểm \( M’, N’ \) lần lượt là các điểm đối xứng của \( M, N \) qua tâm đường tròn. Tìm số đo của cung \( \widehat{AM’} \), \( \widehat{AN’} \) và \( \widehat{M’N’} \).
Lời giải
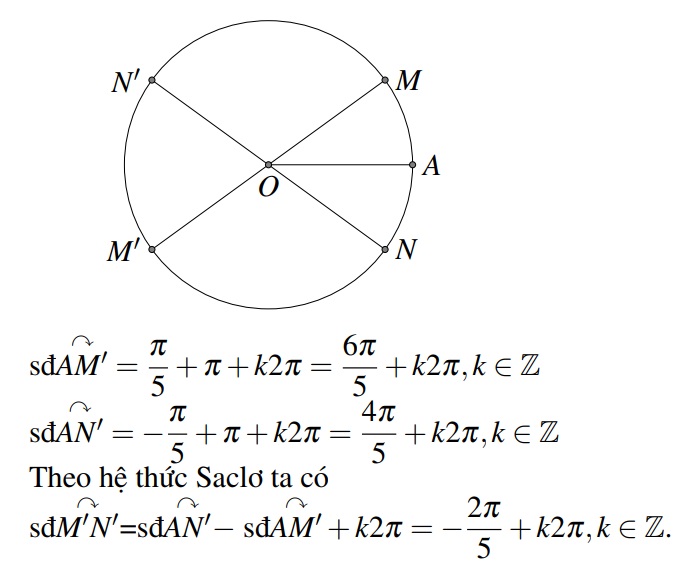
Hiểu về độ dài cung lượng giác giúp chúng ta nắm vững mối quan hệ giữa góc, bán kính và độ dài cung tròn. Kiến thức này không chỉ quan trọng trong học tập mà còn có nhiều ứng dụng thực tế, từ tính toán hình học đến các lĩnh vực đời sống.