Trong chương Lượng giác, rút gọn biểu thức lượng giác là một dạng bài quan trọng, thường xuyên xuất hiện trong kiểm tra và đề thi THPT. Dạng bài tập toán này giúp bạn vận dụng các công thức lượng giác để biến đổi biểu thức phức tạp về dạng đơn giản hơn — nhờ đó tìm ra kết quả nhanh và chính xác.
1. Kiến thức cần nhớ để rút gọn biểu thức lượng giác
Các công thức cơ bản
Một số công thức được dùng thường xuyên khi rút gọn:
$\sin^2 x + \cos^2 x = 1$
$1 + \tan^2 x = \frac{1}{\cos^2 x}$
$1 + \cot^2 x = \frac{1}{\sin^2 x}$
Công thức hạ bậc:
$\sin^2 x = \frac{1 – \cos 2x}{2} \quad ; \quad \cos^2 x = \frac{1 + \cos 2x}{2}$
Khi làm bài tập dạng này, học sinh thường gặp những biểu thức có chứa $\sin^2 x$ hoặc $\cos^2 x$. Để biến đổi chúng về dạng đơn giản hơn, công thức hạ bậc là công cụ không thể thiếu. Nếu bạn chưa nắm vững phần này, hãy xem lại bài công thức hạ bậc lượng giác trước khi bắt đầu luyện tập.
Công thức nhân đôi:
$\sin 2x = 2\sin x\cos x \quad ; \quad \cos 2x = \cos^2 x – \sin^2 x$
Công thức biến đổi tích – tổng:
$\sin a \cos b = \frac{1}{2}[\sin(a + b) + \sin(a – b)]$
$\cos a \cos b = \frac{1}{2}[\cos(a + b) + \cos(a – b)]$
$\sin a \sin b = \frac{1}{2}[\cos(a – b) – \cos(a + b)]$
Một trong những kỹ năng quan trọng khi làm bài tập lượng giác là biết cách biến đổi tích thành tổng. Các biểu thức như $\sin a \cos b$ hay $\cos a \cos b$ đều có thể rút gọn nhanh bằng công thức nhân lượng giác. Nếu bạn chưa quen, hãy đọc lại bài công thức nhân lượng giác để ôn lại công thức và ví dụ minh họa.
2. Các dạng bài tập rút gọn biểu thức lượng giác
Dạng 1. Rút gọn biểu thức cơ bản
Sử dụng trực tiếp các công thức lượng giác quen thuộc.
Ví dụ 1: Rút gọn biểu thức: $P = \sin^2 x + \cos^2 x$
Lời giải
Vì $\sin^2 x + \cos^2 x = 1$ nên $P = 1$.
Dạng 2. Dùng công thức nhân đôi hoặc hạ bậc
Khi biểu thức có bậc cao hoặc xuất hiện $\sin^2$, $\cos^2$.
Ví dụ 2: Rút gọn: $A = 1 – 2\sin^2 x$
Lời giải
Áp dụng $\cos 2x = 1 – 2\sin^2 x$ ⇒ $A = \cos 2x$
Dạng 3. Biến đổi tích thành tổng
Ví dụ 3: Rút gọn: $B = \sin x \cos x$
Lời giải
$\sin x \cos x = \frac{1}{2}\sin 2x$
Dạng 4. Kết hợp nhiều công thức
Ví dụ 4: Rút gọn: $C = \frac{1 – \cos 2x}{1 + \cos 2x}$
Lời giải
$\frac{1 – \cos 2x}{1 + \cos 2x} = \frac{2\sin^2 x}{2\cos^2 x} = \tan^2 x$
Dạng 5. Dạng nâng cao tổng hợp
Ví dụ 5: Rút gọn: $D = \frac{\sin^4 x – \cos^4 x}{\sin^2 x – \cos^2 x}$
Lời giải
$\sin^4 x – \cos^4 x = (\sin^2 x – \cos^2 x)(\sin^2 x + \cos^2 x)$
Vì $\sin^2 x + \cos^2 x = 1$ nên $D = 1$
3. Mẹo làm nhanh dạng rút gọn biểu thức lượng giác
- Nhận dạng nhanh công thức quen thuộc:
Khi thấy biểu thức chứa $\sin^2$ hoặc $\cos^2$ → nghĩ ngay đến công thức hạ bậc. - Nếu có tích giữa sin và cos → nghĩ tới công thức nhân đôi hoặc biến đổi tích – tổng.
- Nếu có dạng $\frac{1 – \cos 2x}{1 + \cos 2x}$ → nên chia cả tử và mẫu cho $\cos^2 x$ để xuất hiện $\tan x$.
- Luôn thử rút gọn dần từng bước thay vì cố nhìn kết quả cuối ngay.
4. Các bài tập thường gặp
Bài tập 1. Rút gọn \(1 – 2\sin^2x\)
Lời giải
$1 – 2{\sin ^2}x$ $ = 1 – 2 \cdot \frac{{1 – \cos 2x}}{2}$ $ = 1 – (1 – \cos 2x)$ $ = 1 – 1 + \cos 2x$ $ = \cos 2x$
Bài tập 2. Cho \( \cot \left( \frac{2017\pi}{2} + x \right) = \frac{1}{2} \). Tính giá trị của biểu thức $P = \frac{2\sin^2{x} + 3\sin{x} \cos{x} – \cos^2{x}}{\cos^2{x} – 3\sin^2{x}}.$
Lời giải
Ta có: $\cot \left( {\frac{{2017\pi }}{2} + x} \right)$ $ = \cot \left( {1008\pi + \frac{\pi }{2} + x} \right)$ $ = \cot \left( {\frac{\pi }{2} + x} \right)$ $ = – \tan x.$
$ \Rightarrow \tan x = – \frac{1}{2}.$
$ \Rightarrow P = \frac{{2{{\tan }^2}x + 3\tan x – 1}}{{1 – 3{{\tan }^2}x}} = – 8$
Bài tập 3. Rút gọn \(\sin^2x – \sin^2y\)
Lời giải
${\sin ^2}x – {\sin ^2}y$ $ = \left( {\frac{{1 – \cos 2x}}{2}} \right) – \left( {\frac{{1 – \cos 2y}}{2}} \right)$ $ = \frac{{1 – \cos 2x – 1 + \cos 2y}}{2}$ $ = \frac{{\cos 2y – \cos 2x}}{2}$ $ = \sin (x + y)\sin (x – y)$
Bài tập 4. Rút gọn biểu thức \( N = \sqrt{\sin^2{x} (4 + \cot{x}) + \cos^2{x} (1 + 3\tan{x})} \).
Lời giải
$ N = \sqrt{4\sin^2{x} + \sin^2{x} \cot{x} + \cos^2{x} + 3\cos^2{x} \tan{x}} $
$ = \sqrt{4\sin^2{x} + \sin^2{x} \cdot \frac{\cos{x}}{\sin{x}} + \cos^2{x} + 3\cos^2{x} \cdot \frac{\sin{x}}{\cos{x}}} $
$ = \sqrt{4\sin^2{x} + 4\sin{x} \cos{x} + \cos^2{x}} $
$ = \sqrt{(2\sin{x} + \cos{x})^2} $ $ = |2\sin{x} + \cos{x}|. $
Bài tập 5. Rút gọn \(\frac{1 – \cos 2x}{1 + \cos 2x}\)
Lời giải
$\frac{{1 – \cos 2x}}{{1 + \cos 2x}}$ $ = \frac{{2{{\sin }^2}x}}{{2{{\cos }^2}x}}$ $ = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}$ $ = {\tan ^2}x$.
Bài tập 6. Rút gọn \(\cos^4x – \sin^4x\)
Lời giải
${\cos ^4}x – {\sin ^4}x$ $ = ({\cos ^2}x – {\sin ^2}x)({\cos ^2}x + {\sin ^2}x)$ $ = ({\cos ^2}x – {\sin ^2}x) \cdot 1$ $ = \cos 2x$
Bài tập 7. Cho \( 6\cos^2{\alpha} + \cos{\alpha} – 2 = 0 \). Biết $ A = \frac{2\sin{\alpha} \cos{\alpha} – \sin{\alpha}}{2\cos{\alpha} – 1} = a + b\tan{\alpha} \text{ với } a, b \in \mathbb{Q}. $ Tính giá trị của biểu thức \( a + b \).
Lời giải
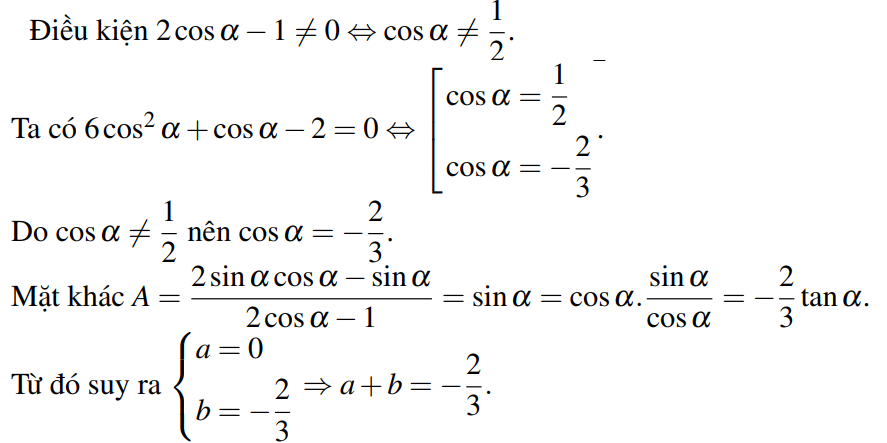
5. Bài tập tự luyện (có đáp án)
| STT | Bài tập | Gợi ý / Đáp án |
|---|---|---|
| 1 | $\frac{1 – \cos 2x}{\sin 2x}$ | $=\tan x$ |
| 2 | $\sin^4 x + \cos^4 x$ | $=1 – \frac{1}{2}\sin^2 2x$ |
| 3 | $\frac{1 + \tan^2 x}{1 – \tan^2 x}$ | $=\frac{1}{\cos 2x}$ |
| 4 | $\sin 3x \cos 2x$ | $=\frac{1}{2}[\sin 5x + \sin x]$ |
| 5 | $\sin^2 x – \cos^2 x$ | $=-\cos 2x$ |
| 6 | $\frac{\sin x + \tan x}{\cos x + 1}$ | $=\tan\frac{x}{2}$ |
| 7 | $\sin^6 x + 3\cos^2 x\sin^4 x + 3\cos^4 x\sin^2 x + \cos^6 x$ | $=1$ |
| 8 | $\sin^2 x \cos^2 x$ | $=\frac{1}{4}\sin^2 2x$ |
| 9 | $\frac{1 – \sin 2x}{\cos 2x}$ | $=\tan(x – 45^\circ)$ |
| 10 | $\frac{\tan x – \sin x}{\sin^3 x}$ | Dạng nâng cao, khuyến khích tự giải |
6. FAQs
Cách nhanh nhất là nhận dạng mẫu và áp dụng công thức quen thuộc như $\sin^2x + \cos^2x = 1$ hoặc $\sin 2x = 2\sin x \cos x$ để giảm bậc hoặc biến đổi tích – tổng.
Các công thức được dùng nhiều nhất gồm:
$\sin^2x + \cos^2x = 1$
$1 + \tan^2x = \frac{1}{\cos^2x}$
$\sin 2x = 2\sin x \cos x$
$\cos 2x = \cos^2x – \sin^2x$
Dùng công thức hạ bậc khi gặp các lũy thừa như $\sin^2x$ hoặc $\cos^2x$, ví dụ:
$\sin^2x = \frac{1 – \cos 2x}{2}$,
$\cos^2x = \frac{1 + \cos 2x}{2}.$
Hãy dùng công thức nhân lượng giác: $\sin A \cos B = \frac{1}{2}[\sin(A + B) + \sin(A – B)].$
Nó giúp chuyển tích thành tổng, biểu thức gọn hơn rất nhiều.
Không cần. Bạn chỉ cần nắm chắc các công thức nền:
$\sin^2x + \cos^2x = 1$,
$\sin 2x = 2\sin x \cos x$,
$\cos 2x = 1 – 2\sin^2x.$
Những công thức này chiếm tới 80% bài rút gọn.
Có thể dùng máy tính để kiểm tra giá trị tại một điểm cụ thể, giúp xác nhận kết quả rút gọn đúng hay sai, nhưng không thể rút gọn biểu thức đại số bằng máy được.
Khi có nhiều biến như $\sin a \cos b$ hoặc $\cos a \cos b$, hãy dùng công thức: $\cos A \cos B = \frac{1}{2}[\cos(A + B) + \cos(A – B)].$
Rút gọn giúp biểu thức trở nên dễ nhận dạng hơn, ví dụ chuyển $2\sin x \cos x$ thành $\sin 2x$ giúp giải nhanh phương trình lượng giác có chứa nhiều ẩn.
Kết luận, dạng bài tập rút gọn biểu thức lượng giác không chỉ là nền tảng quan trọng trong chương trình toán học mà còn đóng vai trò cốt lõi trong việc học tốt lượng giác. Việc nắm vững các công thức như nhân đôi, hạ bậc, cộng trừ góc giúp học sinh giải quyết nhanh chóng các bài toán phức tạp. Đây là kỹ năng không thể thiếu, góp phần xây dựng nền tảng vững chắc cho việc học toán lượng giác nâng cao sau này.
