Tổng hợp các bài toán thực tế chương Hàm số lượng giác và Phương trình lượng giác, phân dạng rõ ràng, giải chi tiết, dễ hiểu, sát đề thi.
Bài toán 1: Một chất điểm dao động điều hoà theo phương trình $s=3\text{sin}\left( \frac{\pi }{2}t \right)$ với $s$ tính bằng $\text{cm}$ và $t$ tính bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm $t$ nào trong 4 giây đầu thì $s\le -\frac{3}{2}$.
Lời giải
Trong 4 giây đầu, ta có $0\le t\le 4$, suy ra $0\le \frac{\pi }{2}t\le 2\pi $.
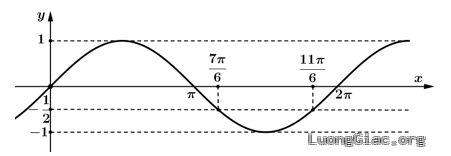
Đặt $x=\frac{\pi }{2}t$, khi đó $x\in \left[ 0;2\pi \right]$. Đồ thị của hàm số $y=\text{sin}x$ trên đoạn $\left[ 0;2\pi \right]$ như sau:
Dựa vào đồ thị trên đoạn $\left[ 0;2\pi \right]$ ta có: $s\le -\frac{3}{2}$ khi $3\text{sin}x\le -\frac{3}{2}$ hay $\text{sin}x\le -\frac{1}{2}$
Suy ra $\frac{7\pi }{6}\le x\le \frac{11\pi }{6}$ nên do đó $\frac{7}{3}\le t\le \frac{11}{3}$.
Bài toán 2: Trong hình minh hoạ dưới đây, cây xanh $AB$ nằm trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao $5\text{ }\!\!~\!\!\text{ m}$. Bóng của cây là $BE$. Vào ngày xuân phân và hạ phân, điểm $E$ di chuyển trên đường thẳng $Bx$. Góc thiên đinh ${{\theta }_{x}}=\left( AB,AE \right)$ phụ thuộc vào vị trí của Mặt Trời và thay đổi theo thời gian trong ngày theo công thức: ${{\theta }_{s}}\left( t \right)=\frac{\pi }{12}\left( t-12 \right)\text{rad}$, với $t$ là thời gian trong ngày (theo đơn vị giờ, $6<t<18)$.
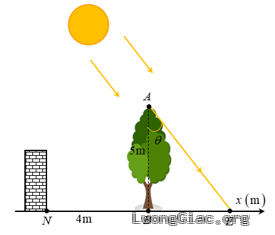
a) Viết hàm số biểu diễn toạ độ của điểm $E$ trên trục $Bx$ theo $t$.
b) Dựa vào đồ thị hàm số tang, hãy xác định các thời điềm mà tại đó bóng cây phủ qua vị trí tường rào $N$ biết $N$ nằm trên trục $Bx$ với toạ độ là ${{x}_{N}}=-4\left( \text{ }\!\!~\!\!\text{ m} \right)$. Làm tròn kết quả đến hàng phần mười.
Lời giải
a) Xét tam giác $ABE$ vuông tại $B$ ta có:$\text{tan}{{\theta }_{s}}\left( t \right)=\frac{BE}{AB}\Leftrightarrow BE=5\text{tan}\left( \frac{\pi }{12}\left( t-12 \right) \right)\text{. }\!\!~\!\!\text{ }$
b) Đồ thị của hàm số ${{\theta }_{s}}=5\text{tan}\left( \frac{\pi }{12}\left( t-12 \right) \right)$
Dựa vào đồ thị hàm số để ${{\theta }_{s}}=5\text{tan}\left( \frac{\pi }{12}\left( t-12 \right) \right)<-4$ và $6<t<18$ suy ra các thời điểm để bóng cây phủ qua hàng rào $N$ là $6<\text{t}<9,4$.
Bài toán 3: Trong hình minh hoạ dưới đây, một ngọn đèn trên hải đăng $H$ cách bờ biển $y{y}’$ một khoảng $HO=1\text{ }\!\!~\!\!\text{ km}$. Đèn xoay ngược chiều kim đồng hồ với tốc độ $\frac{\pi }{10}\text{rad}/\text{s}$ và chiếu hai luồng ánh sáng về hai phía đối diện nhau. Khi đèn xoay, điểm $M$ mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển động dọc theo bờ.
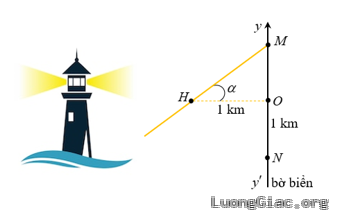
a) Ban đầu luồng sáng trùng với đường thẳng $HO$. Viết hàm số biểu thị toạ độ ${{y}_{M}}$ của điểm $M$ trên trục $Oy$ theo thời gian $t$.
b) Ngôi nhà $N$ nằm trên bờ biển với toạ độ ${{y}_{N}}=-1\left( \text{ }\!\!~\!\!\text{ km} \right)$. Xác định các thời điểm $t$ mà đèn hải đăng chiếu vào ngôi nhà.
Lời giải
a) Sau $t$ giây điểm $M$ quét được một góc lượng giác có số đo là: $\alpha =\frac{\pi }{10}t$ rad.
Xét tam giác $HOM$ vuông tại $O$ có: $MO=\text{tan}\alpha .1=\text{tan}\left( \frac{\pi }{10}t \right)$. Vậy tọa độ ${{y}_{M}}=\text{tan}\left( \frac{\pi }{10}t \right)$.
b) Xét $\text{tan}\left( \frac{\pi }{10}t \right)=-1$$\Leftrightarrow \text{tan}\left( \frac{\pi }{10}t \right)=\text{tan}\left( -\frac{\pi }{4} \right)$$\Leftrightarrow \frac{\pi }{10}t=-\frac{\pi }{4}+k\pi $$\Leftrightarrow t=-2,5+10k,k\in \mathbb{Z}$
Vì t $\ge 0$ nên tại các thời điểm $t=-2,5+10k,k\in \mathbb{Z},k\ge 1$ thì đèn hải đăng chiếu vào ngôi nhà.
Vậy phương trình đã cho có các nghiệm là $x=-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}$ và $x=-\frac{\pi }{10}+k\frac{\pi }{5},k\in \mathbb{Z}$
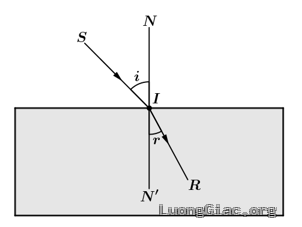
Bài toán 4: Theo Định luật khúc xạ ánh sáng, khi một tia sáng được chiếu tới mặt phân cách giữa hai môi trường trong suốt không đồng chất thì tỉ số $\frac{\text{sin}i}{\text{sin}r}$, với $i$ là góc tới và $r$ là góc khúc xạ, là một hằng số phụ thuộc vào chiết suất của hai môi trường. Biết rằng khi góc tới là ${{45}^{\circ }}$ thì góc khúc xạ bằng ${{30}^{\circ }}$. Khi góc tới là ${{60}^{\circ }}$ thì góc khúc xạ là bao nhiêu? Làm tròn kết quả đến hàng phần trăm.
Lời giải
Vì $\frac{\text{sin}{{45}^{\circ }}}{\text{sin}{{30}^{\circ }}}=\frac{\text{sin}{{60}^{\circ }}}{\text{sin}r}$ nên $\text{sin}r=\frac{\text{sin}{{60}^{\circ }}\text{sin}{{30}^{\circ }}}{\text{sin}{{45}^{\circ }}}=\frac{\sqrt{6}}{4}$. Suy ra $r={{37,76}^{\circ }}$.
Bài toán 5: Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên. Trong mặt phẳng toạ độ $Oxy$, chọn điểm có tọa độ $\left( O;{{y}_{0}} \right)$ là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là:
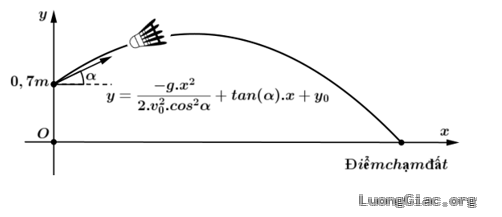
$y=\frac{-g.{{x}^{2}}}{2.v_{0}^{2}.{{\cos }^{2}}\alpha }+\tan \alpha .x+{{y}_{0}}$; trong đó:
$g$ là gia tốc trọng trường (thường được chọn là $9,8~m/{{s}^{2}}$)
$\alpha $ là góc phát cầu (so với phương ngang của mặt đất)
${{v}_{0}}$ là vận tốc ban đầu của cầu
${{y}_{0}}$ là khoảng cách từ vị trí phát cầu đến mặt đất.
Đây là một hàm số bậc hai nên quỹ đạo chuyển động của cầu lông là một parabol.
Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là $6,68~$m. Quan sát hình bên dưới, hỏi người chơi đã phát cầu góc khoảng bao nhiêu độ so với mặt đất? ( biết cầu rời mặt vợt ở độ cao $0,7~$m so với mặt đất và vận tốc xuất phát của cầu là $8~$m/s, bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng phẳng đứng).
Lời giải
Với $g=9,8~m/{{s}^{2}}$, vận tốc ban đầu ${{v}_{0}}=8~m/s$ thì phương trình quỹ đạo của cầu:
$y=\frac{-g.{{x}^{2}}}{2.v_{0}^{2}.{{\cos }^{2}}\alpha }+\tan \alpha .x+{{y}_{0}}$
Khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là $6,68~$m nghĩa là $x=6,68~$m.
Ta có: $\frac{{ – 9,8.{{\left( {6,68} \right)}^2}}}{{128.{{\cos }^2}\alpha }} + \tan \left( \alpha \right).\left( {6,68} \right) + 0,7 = 0$ $ \Leftrightarrow \frac{{ – 9,8.{{\left( {6,68} \right)}^2}}}{{128}}\left( {1 + {{\tan }^2}\alpha } \right)$ $ + \tan \left( \alpha \right).\left( {6,68} \right)$ $ + 0,7 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} { \tan \alpha \approx 1,378}\\ { \tan \alpha \approx 0,576} \end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {\alpha \simeq 54,04^\circ }\\ {\alpha \simeq 29,97^\circ } \end{array}} \right.$
Vậy người chơi đã phát cầu một góc gần ${{54}^{0}}$ hoặc gần ${{30}^{{}^\circ }}$ so với mặt đất.
Bài toán 6: Một vệ tinh bay quanh Trái Đất theo một quỹ đạo hình Elip (như hình vẽ):
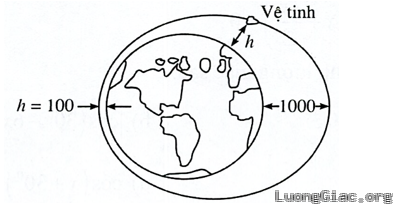
Độ cao $h$ (tính bằng kilômet) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức $h=550+450\cdot \cos \frac{\pi }{50}t$. Trong đó $t$ là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Người ta cần thực hiện một thí nghiệm khoa học khi vệ tinh cách mặt đất $250~km$. Trong khoảng 60 phút đầu tiên kể từ lúc vệ tinh bay vào quỹ đạo, hãy tìm thời điểm để có thể thực hiện thí nghiệm đó?
Lời giải
Ta có phương trình: $550 + 450 \cdot \cos \frac{\pi }{{50}}t = 250$ $ \Leftrightarrow \cos \frac{\pi }{{50}}t = – \frac{2}{3}$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {\frac{\pi }{{50}}t \approx 2,3 + k2\pi }\\ {\frac{\pi }{{50}}t \approx – 2,3 + k2\pi } \end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {t \approx 36,61 + k100}\\ {t \approx – 36,61 + k100} \end{array},k \in Z.} \right.$
Vậy trong khoảng 60 phút đầu tiên kể từ lúc vệ tinh bay vào quỹ đạo, tại thời điểm $t\approx 36,61$ (phút) thì ta có thể thực hiện thí nghiệm đó.
Skip to PDF content