Lượng giác giúp bạn khám phá mối quan hệ giữa các góc và cạnh trong hình học. Trong đó, bài tập công thức cộng lượng giác là như một công cụ quan trọng, giúp biến đổi tổng hoặc hiệu của các hàm lượng giác như sin, cos, tan thành những biểu thức đơn giản và dễ xử lý hơn. Bài viết này sẽ giúp bạn không chỉ nhớ lại những công thức cộng lượng giác, còn rèn luyện cách sử dụng công thức vào giải bài tập lượng giác lớp 10 hiệu quả.
1. Các công thức cộng lượng giác sin cos tan
Để giải các bài toán liên quan đến các công thức cộng, ta thường sử dụng các công thức sau:
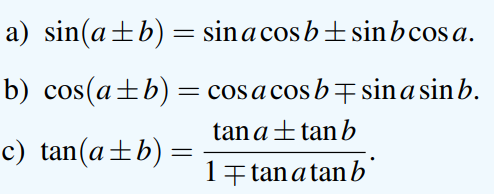
Những công thức này cho phép biến đổi linh hoạt, từ đó giải quyết hiệu quả các bài toán về tổng hoặc hiệu góc.
2. Bài tập vận dụng
Bài tập 1. Tính giá trị của biểu thức
$P = \cos 10^\circ + \cos 11^\circ \cos 21^\circ + \cos 69^\circ \cos 79^\circ.$
Lời giải
Ta có
$P = \cos {10^0} + \cos {11^0}\cos {21^0} + \sin {11^0}\cos {21^0}$ $ = \cos {10^0} + \cos ({11^0} – {21^0})$ $ = 2\cos {10^0}$
Bài tập 2. Không sử dụng MTCT, hãy tính giá trị \( \sin 15^\circ \), \( \cos 15^\circ \), \( \sin 75^\circ \) và \( \cos 75^\circ \).
Lời giải
$ \sin 15^\circ = \sin (45^\circ – 30^\circ) = \sin 45^\circ \cos 30^\circ – \sin 30^\circ \cos 45^\circ = \frac{\sqrt{6} – \sqrt{2}}{4}. $
$ \cos 15^\circ = \cos (45^\circ – 30^\circ) = \cos 45^\circ \cos 30^\circ + \sin 45^\circ \sin 30^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}. $
$ \sin 75^\circ = \sin (45^\circ + 30^\circ) = \sin 45^\circ \cos 30^\circ + \sin 30^\circ \cos 45^\circ = \frac{\sqrt{6} + \sqrt{2}}{4}. $
$ \cos 75^\circ = \cos (45^\circ + 30^\circ) = \cos 45^\circ \cos 30^\circ – \sin 45^\circ \sin 30^\circ = \frac{\sqrt{6} – \sqrt{2}}{4}. $
Bài tập 3. Rút gọn các biểu thức:
a) $ A = \frac{\sqrt{2} \cos a – 2\cos \left(\frac{\pi}{4} + a\right)}{-\sqrt{2} \sin a + 2\sin \left(\frac{\pi}{4} + a\right)}. $
b) $ B = (\tan a – \tan b) \cot (a – b) – \tan a \tan b. $
Lời giải
a) Ta có
$ A = \frac{\sqrt{2} \cos a – 2 \left( \cos a – \sin \frac{\pi}{4} \sin a \right)}{-\sqrt{2} \sin a + 2 \left( \sin a + \cos \frac{\pi}{4} \sin a \right)} $ $ = \frac{\sqrt{2} \sin a}{\sqrt{2} \cos a} = \tan a. $
b) Ta có $ B = \tan (a – b) (1 + \tan a \tan b) \cot (a – b) – \tan a \tan b = 1. $
Bài tập 4. Rút gọn biểu thức \( P = \frac{\sin\left(\frac{\pi}{4} – a\right) + \cos\left(\frac{\pi}{4} – a\right)}{\sin\left(\frac{\pi}{4} – a\right) – \cos\left(\frac{\pi}{4} – a\right)}. \)
Lời giải
$ P = \frac{\sin \frac{\pi}{4} \cos a – \cos \frac{\pi}{4} \sin a + \cos \frac{\pi}{4} \cos a + \sin \frac{\pi}{4} \sin a} {\sin \frac{\pi}{4} \cos a – \cos \frac{\pi}{4} \sin a – \cos \frac{\pi}{4} \cos a – \sin \frac{\pi}{4} \sin a} $
$ = \frac{\sqrt{2} \cos a}{-\sqrt{2} \sin a} = -\cot a. $
Bài tập 5. Cho tam giác \( ABC \), chứng minh rằng: $ \tan A + \tan B + \tan C = \tan A \tan B \tan C. $
Lời giải
Ta có:
$\tan A + \tan B + \tan C = \frac{\sin A}{\cos A} + \frac{\sin B}{\cos B} + \frac{\sin C}{\cos C}$
$= \frac{\sin A \cos B + \sin B \cos A}{\cos A \cos B} + \frac{\sin C}{\cos C}$
$= \frac{\sin (A + B)}{\cos A \cos B} + \frac{\sin C}{\cos C}$
$= \frac{\sin C}{\cos A \cos B} + \frac{\sin C}{\cos C}$
$= \sin C \left(\frac{1}{\cos A \cos B} + \frac{1}{\cos C} \right)$
$= \sin C \cdot \frac{\cos A \cos B + \cos C}{\cos A \cos B \cos C}$
$= \tan C \cdot \frac{\cos A \cos B + \cos C}{\cos A \cos B}$
$= \tan C \cdot \frac{\cos A \cos B – \cos (A + B)}{\cos A \cos B}$
$ = \tan C \cdot \frac{\cos A \cos B – \cos A \cos B + \sin A \sin B}{\cos A \cos B} $
$ = \tan C \cdot \frac{\sin A \sin B}{\cos A \cos B} $
$ = \tan A \tan B \tan C. $
Bài tập 6. Cho \( a + b = \frac{\pi}{4} \), chứng minh rằng $ (1 + \tan a)(1 + \tan b) = 2. $
Lời giải
Ta có: $ (1 + \tan a)(1 + \tan b) = (1 + \tan a) \left( 1 + \tan \left( \frac{\pi}{4} – a \right) \right). $
Sử dụng công thức: $ \tan (\frac{\pi}{4} – a) = \frac{1 – \tan a}{1 + \tan a}, $ ta được: $ (1 + \tan a) \left( 1 + \frac{1 – \tan a}{1 + \tan a} \right). $
Biểu thức trong ngoặc đơn trở thành: $ 1 + \frac{1 – \tan a}{1 + \tan a} = \frac{(1 + \tan a) + (1 – \tan a)}{1 + \tan a} = \frac{2}{1 + \tan a}. $
Do đó: $ (1 + \tan a) \cdot \frac{2}{1 + \tan a} = 2. $
Vậy đẳng thức đã được chứng minh.
Bài tập 7. Tính \( \alpha + \beta \) biết \( \tan \alpha = \frac{2}{5}, \tan \beta = \frac{3}{7} \) với \( 0 < \alpha, \beta < \frac{\pi}{2} \).
Lời giải
Ta có:$\tan (\alpha + \beta) = \frac{\tan \alpha + \tan \beta}{1 – \tan \alpha \tan \beta} = 1.$
Do \( 0 < \alpha, \beta < \frac{\pi}{2} \) nên \( 0 < \alpha + \beta < \pi \).
Vậy \( \alpha + \beta = \frac{\pi}{4} \).
Bài tập 8. Tính
a) \( \cos \left( \alpha + \frac{\pi}{3} \right) \), biết \( \sin \alpha = \frac{1}{\sqrt{3}} \) và \( 0 < \alpha < \frac{\pi}{2} \).
b) \( \tan \left( \alpha – \frac{\pi}{4} \right) \), biết \( \cos \alpha = -\frac{1}{3} \) và \( \frac{\pi}{2} < \alpha < \pi \).
c) \( \cos (a + b) \), \( \sin (a – b) \), biết \( \sin a = \frac{4}{5} \), \( 0^\circ < a < 90^\circ \) và \( \sin b = \frac{2}{3} \), \( 90^\circ < b < 180^\circ \).
Lời giải
a) Do \( 0 < \alpha < \frac{\pi}{2} \) nên \( \cos \alpha > 0 \). Do đó:
$\cos \alpha = \sqrt{1 – \sin^2 \alpha} = \sqrt{1 – \frac{1}{3}} = \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3}.$
Ta có:
$ \cos \left( \alpha + \frac{\pi}{3} \right) = \cos \alpha \cos \frac{\pi}{3} – \sin \alpha \sin \frac{\pi}{3} $ $ = \frac{\sqrt{6}}{3} \cdot \frac{1}{2} – \frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{3}}{6} – \frac{1}{2} = \frac{-3 + \sqrt{6}}{6}. $
b) Do \( \frac{\pi}{2} < \alpha < \pi \) nên \( \sin \alpha > 0 \). Do đó:
$\sin \alpha = \sqrt{1 – \cos^2 \alpha} = \sqrt{1 – \left(-\frac{1}{3}\right)^2} = \frac{2\sqrt{2}}{3}.$
Suy ra: $\tan \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{\frac{2\sqrt{2}}{3}}{-\frac{1}{3}} = -2\sqrt{2}.$
Ta có:
$\tan \left( \alpha – \frac{\pi}{4} \right) = \frac{\tan \alpha – \tan \frac{\pi}{4}}{1 + \tan \alpha \tan \frac{\pi}{4}}$
$= \frac{-2\sqrt{2} – 1}{-2\sqrt{2} + 1} = \frac{9 + 4\sqrt{2}}{7}.$
c) Có \( 0^\circ < a < 90^\circ \) nên \( \cos a = \frac{3}{5} \), \( 90^\circ < b < 180^\circ \) nên \( \cos b = -\frac{\sqrt{5}}{3} \).
$\cos (a + b) = \cos a \cos b – \sin a \sin b$
$= \frac{3}{5} \cdot \left(-\frac{\sqrt{5}}{3}\right) – \frac{4}{5} \cdot \frac{2}{3} = \frac{-\sqrt{5}}{5} – \frac{8}{15} = \frac{8 + 3\sqrt{5}}{15}.$
$\sin (a – b) = \sin a \cos b – \cos a \sin b$
$= \frac{4}{5} \cdot \left(-\frac{\sqrt{5}}{3}\right) – \frac{3}{5} \cdot \frac{2}{3} = \frac{-4\sqrt{5}}{15} – \frac{6}{15} = \frac{6 + 4\sqrt{5}}{15}.$
Bài tập 9. Cho \( a – b = \frac{\pi}{4} \), chứng minh rằng $ \frac{1 + \tan b}{1 – \tan b} = \tan a. $
Lời giải
Ta có: $ a – b = \frac{\pi}{4} \iff a = \frac{\pi}{4} + b. $
Do đó: $ \tan a = \tan \left( \frac{\pi}{4} + b \right). $
Sử dụng công thức: $ \tan (x + y) = \frac{\tan x + \tan y}{1 – \tan x \tan y}, $
ta có: $ \tan a = \tan \left( \frac{\pi}{4} + b \right) = \frac{\tan \frac{\pi}{4} + \tan b}{1 – \tan \frac{\pi}{4} \tan b}. $
Vì \( \tan \frac{\pi}{4} = 1 \), nên: $ \tan a = \frac{1 + \tan b}{1 – \tan b}. $
Vậy đẳng thức đã được chứng minh.
Bài tập 10. Cho tam giác \(ABC\), chứng minh rằng $ \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{B}{2} \tan \frac{C}{2} + \tan \frac{C}{2} \tan \frac{A}{2} = 1. $
Lời giải
Ta có $ \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{B}{2} \tan \frac{C}{2} + \tan \frac{C}{2} \tan \frac{A}{2} $ $ = \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{C}{2} \left( \tan \frac{A}{2} + \tan \frac{B}{2} \right). $ $ = \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{C}{2} \tan \frac{(A + B)}{2} \left( 1 – \tan \frac{A}{2} \tan \frac{B}{2} \right). $ $ = \tan \frac{A}{2} \tan \frac{B}{2} + \tan \frac{C}{2} \cot \frac{C}{2} \left( 1 – \tan \frac{A}{2} \tan \frac{B}{2} \right). $ $ = \tan \frac{A}{2} \tan \frac{B}{2} + 1 – \tan \frac{A}{2} \tan \frac{B}{2} = 1. $
Vậy đẳng thức đã được chứng minh.
3. FAQs
Dùng trong rút gọn biểu thức, chứng minh đẳng thức, giải phương trình, tính giá trị biểu thức có góc tổng hoặc hiệu.
$[\cos (a + b) = \cos a\cos b – \sin a\sin b]$
$[\cos (a – b) = \cos a\cos b + \sin a\sin b]$
Kết hợp công thức cộng với các công thức khác như hạ bậc, nhân đôi, tổng thành tích để rút gọn biểu thức phức tạp.
$\begin{array}{l} \tan (a + b) = \frac{{\tan a + \tan b}}{{1 – \tan a\tan b}}\ \tan (a – b) = \frac{{\tan a – \tan b}}{{1 + \tan a\tan b}} \end{array}$
Trong cos(a + b) có dấu trừ giữa hai tích \(\cos a \cos b\) và \(\sin a \sin b\). Trong cos(a – b) là dấu cộng giữa hai tích đó.
Qua bài viết này, chúng ta đã tìm hiểu sâu về các công thức cộng lượng giác như sin, cos, tan – từ những khái niệm cơ bản đến cách áp dụng thực tiễn. Việc nắm chắc các công thức này không chỉ giúp bạn giải quyết bài toán một cách nhanh chóng, mà hiểu hơn về các bài tập lượng giác.