Trong lượng giác, công thức hạ bậc giúp chuyển các biểu thức bậc hai của sin, cos về dạng bậc nhất để tính toán dễ hơn. Đây là công cụ quan trọng khi giải bài tập biến đổi, chứng minh đẳng thức hoặc tính tích phân lượng giác. Bài viết dưới đây hệ thống đầy đủ các công thức hạ bậc sin, cos, sin², cos², sin2x, cos2x, kèm ví dụ minh họa và mẹo ghi nhớ giúp bạn học nhanh và áp dụng hiệu quả.
1. Công thức hạ bậc là gì?
Công thức hạ bậc là nhóm công thức lượng giác giúp biến đổi các biểu thức bậc hai của sin, cos, tan, cot về biểu thức bậc nhất, qua đó đơn giản hóa quá trình tính toán, rút gọn hoặc chứng minh đẳng thức.
Nói cách khác, “hạ bậc” nghĩa là giảm bậc số mũ trong biểu thức lượng giác.
Ví dụ: $\sin^2x = \frac{1 – \cos2x}{2}$ là kết quả của việc “hạ bậc” từ biểu thức $\sin^2x$ (bậc 2) về $\cos2x$ (bậc 1).
Ý nghĩa của phép hạ bậc trong lượng giác
- Giúp rút gọn biểu thức phức tạp thành dạng dễ tính toán hơn.
- Dùng trong chứng minh đẳng thức lượng giác và tính tích phân – đạo hàm lượng giác.
- Là bước trung gian để chuyển đổi giữa các công thức nhân đôi, cộng góc, hoặc biến đổi tích thành tổng.
Khi nào cần sử dụng công thức hạ bậc?
- Khi biểu thức có $\sin^2x$, $\cos^2x$, $\tan^2x$, hoặc $\cot^2x$.
- Khi cần rút gọn phương trình lượng giác bậc cao về dạng cơ bản.
- Khi giải các bài toán cực trị lượng giác trong lớp 11, 12.
2. Các công thức hạ bậc cơ bản
Công thức hạ bậc 2
“hạ bậc 2” nghĩa là giảm bậc của hàm lượng giác từ bậc hai xuống bậc một, giúp biểu thức trở nên đơn giản hơn, thuận tiện cho việc tính toán, chứng minh đẳng thức hoặc giải phương trình lượng giác.
Các công thức biểu diễn \(\sin^2(x)\), \(\cos^2(x)\) và \(\tan^2(x)\) theo hàm số cos của góc gấp đôi.

Từ các công thức trên, ta thấy công thức hạ bậc bậc 2 là một công cụ hiệu quả giúp đơn giản hóa các biểu thức lượng giác nhanh chóng. Tuy nhiên, khi gặp dạng bình phương, việc áp dụng công thức này có một số điểm đặc biệt cần lưu ý, khiến bài toán trở nên thách thức hơn. Để hiểu rõ cách biến đổi và rèn luyện kỹ năng giải, bạn có thể tham khảo bài tập công thức hạ bậc 2 lượng giác với các ví dụ minh họa chi tiết.
Công thức hạ bậc 3
“hạ bậc 3” giúp ta giảm từ bậc ba → bậc một, nhờ đó các biểu thức trở nên dễ xử lý hơn.
Các công thức lượng giác biểu diễn \(\sin^3(x)\), \(\cos^3(x)\) và \(\tan^3(x)\) theo các giá trị của \(\sin(x)\), \(\cos(x)\) và \(\tan(x)\) với bội số của góc \(3x\).
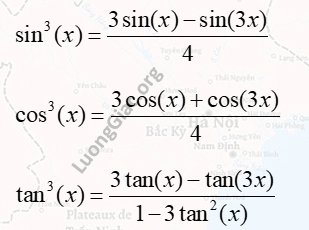
Nếu bạn muốn hiểu sâu hơn về các công thức hạ bậc này, hãy tiếp tục khám phá công thức hạ bậc 3 lượng giác. Nội dung này sẽ giúp bạn rút gọn dễ dàng các biểu thức như sin³x, cos³x và vận dụng linh hoạt khi giải phương trình hoặc biến đổi các dạng bài lượng giác nâng cao.
Công thức hạ bậc 4
“hạ bậc 4” là bước tiếp theo trong chuỗi biến đổi nâng cao, thường gặp trong các bài toán rút gọn biểu thức, tích phân lượng giác, hoặc biến đổi Fourier.
Công thức biểu diễn \(\sin^4(x)\), \(\cos^4(x)\) và \(\tan^4(x)\) theo các giá trị của \(\cos(2x)\) và \(\cos(4x)\).

Ở mức độ cao hơn, bài công thức hạ bậc 4 lượng giác sẽ giúp bạn hiểu sâu hơn về quy luật hạ bậc của các hàm sin và cos. Việc nắm chắc phần này không chỉ giúp bạn rút gọn biểu thức hiệu quả mà còn tạo nền tảng vững chắc cho các bài toán tổng hợp.
Công thức hạ bậc 5
Hạ bậc 5 là bước mở rộng của “chuỗi công thức hạ bậc” — từ bậc 2, 3, 4 đến bậc 5 — giúp đưa mọi biểu thức lượng giác bậc cao về dạng đơn giản hơn để dễ xử lý.
Công thức lượng giác biểu diễn \(\sin^5(x)\), \(\cos^5(x)\) và \(\tan^5(x)\) theo các giá trị của \(\sin(x)\), \(\cos(x)\) và \(\tan(x)\) với bội số của góc \(3x\) và \(5x\).
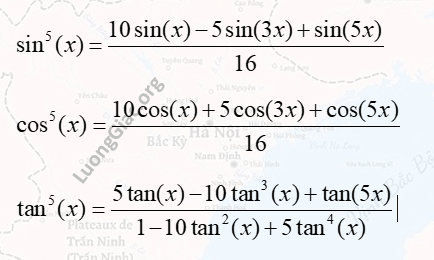
Để làm chủ các dạng lượng giác này, đừng bỏ qua bài công thức hạ bậc 5 lượng giác. Nội dung này không chỉ giúp bạn rút gọn các biểu thức bậc cao mà còn cung cấp quy luật hệ số giúp ghi nhớ công thức nhanh chóng.
Công thức tổng quát cho \(\sin^n(x)\) và \(\cos^n(x)\) với \(n\) chẵn
Khi \(n\) là số chẵn, ta có thể biểu diễn \(\sin^n(x)\) và \(\cos^n(x)\) dưới dạng tổng của các hàm cos với bội góc chẵn \(0, 2x, 4x, …, nx\). Công thức tổng quát:

Công thức tổng quát cho \(\sin^n(x)\) và \(\cos^n(x)\) với \(n\) lẻ
Khi n là số lẻ, ta không thể hạ bậc trực tiếp như trường hợp chẵn, nhưng vẫn có công thức tổng quát biểu diễn \(\sin^n x\) và \(\cos^n x\) dưới dạng tổng các hàm sin (hoặc cos) với bội góc lẻ.

Công thức hạ bậc cho 2x, 3x, 4x, 5x:
Đây là các công thức nhân đôi trong lượng giác, giúp biểu diễn \(\sin(2x)\), \(\cos(2x)\) và \(\tan(2x)\) theo các giá trị của \(\sin(x)\), \(\cos(x)\) và \(\tan(x)\).
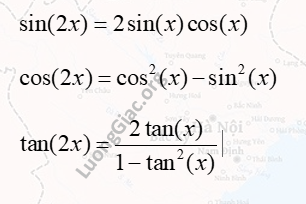
Công thức cho sin(3x), cos(3x), tan(3x)
Đây là các công thức lượng giác bội số giúp biểu diễn \(\sin(3x)\), \(\cos(3x)\) và \(\tan(3x)\) theo các giá trị của \(\sin(x)\), \(\cos(x)\) và \(\tan(x)\).
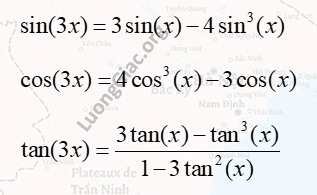
Công thức cho sin(4x), cos(4x), tan(4x)
Đây là các công thức lượng giác giúp biểu diễn \(\sin(4x)\), \(\cos(4x)\) và \(\tan(4x)\) theo các giá trị của \(\sin(x)\), \(\cos(x)\) và \(\tan(x)\).
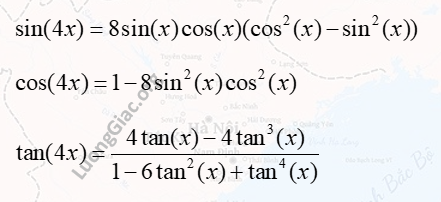
Công thức cho sin(5x), cos(5x), tan(5x)
Đây là các công thức lượng giác giúp biểu diễn \(\sin(5x)\), \(\cos(5x)\) và \(\tan(5x)\) theo các giá trị của \(\sin(x)\), \(\cos(x)\) và \(\tan(x)\).

3. Bảng tổng hợp công thức
| Biểu thức | Dạng hạ bậc | Ghi chú |
|---|---|---|
| $\sin^2x$ | $\frac{1 – \cos2x}{2}$ | Suy ra từ $\cos2x = 1 – 2\sin^2x$ |
| $\cos^2x$ | $\frac{1 + \cos2x}{2}$ | Suy ra từ $\cos2x = 2\cos^2x – 1$ |
| $\tan^2x$ | $\frac{1 – \cos2x}{1 + \cos2x}$ | Từ $\tan^2x = \frac{\sin^2x}{\cos^2x}$ |
| $\cot^2x$ | $\frac{1 + \cos2x}{1 – \cos2x}$ | Từ $\cot^2x = \frac{\cos^2x}{\sin^2x}$ |
💡 Mẹo nhỏ: Hai công thức đầu (sin²x và cos²x) là trọng tâm nhất – thường xuất hiện trong bài rút gọn, chứng minh hoặc tích phân lượng giác.
4. Cách ghi nhớ nhanh
Suy luận từ công thức nhân đôi
Nếu nhớ được công thức nhân đôi: $ \cos2x = 1 – 2\sin^2x \quad \text{và} \quad \cos2x = 2\cos^2x – 1 $
Thì chỉ cần “đảo ngược” lại là ra công thức hạ bậc: $ \sin^2x = \frac{1 – \cos2x}{2}, \quad \cos^2x = \frac{1 + \cos2x}{2} $
Mẹo học thuộc nhanh bằng mối liên hệ sin ↔ cos
- $\sin^2x$: dấu trừ trước $\cos2x$.
- $\cos^2x$: dấu cộng trước $\cos2x$.→ Chỉ cần nhớ “sin trừ – cos cộng”, bạn sẽ không bao giờ nhầm.
So sánh với công thức cộng góc
Trong khi công thức cộng góc (ví dụ: $\cos(a+b)$) tăng góc, thì công thức hạ bậc giảm góc xuống 2x.
Cả hai nhóm này liên hệ chặt chẽ — nắm được một, bạn dễ dàng suy ra nhóm còn lại.
5. Bài tập
Bài tập 1. Biến đổi $2\sin^2x + 3\cos^2x$.
Lời giải
Thay $\sin^2x$ và $\cos^2x$ bằng công thức hạ bậc:
- $\sin^2x = \frac{1 – \cos 2x}{2}$,
- $\cos^2x = \frac{1 + \cos 2x}{2}$.
Thay vào biểu thức: $2\sin^2x + 3\cos^2x = 2 \cdot \frac{1 – \cos 2x}{2} + 3 \cdot \frac{1 + \cos 2x}{2}$.
$= \frac{2(1 – \cos 2x)}{2} + \frac{3(1 + \cos 2x)}{2} = 1 – \cos 2x + \frac{3 + 3\cos 2x}{2}$.
$= 1 – \cos 2x + \frac{3}{2} + \frac{3\cos 2x}{2}$.
$= 1 + \frac{3}{2} – \cos 2x + \frac{3\cos 2x}{2} = \frac{5}{2} + \frac{-2\cos 2x + 3\cos 2x}{2} = \frac{5}{2} + \frac{\cos 2x}{2}$.
Vậy: $2\sin^2x + 3\cos^2x = \frac{5}{2} + \frac{\cos 2x}{2}$.
Bài tập 2. Biến đổi $\sin^2x \cos^2x$.
Lời giải
Thay $\sin^2x = \frac{1 – \cos 2x}{2}$ và $\cos^2x = \frac{1 + \cos 2x}{2}$:
$\sin^2x \cos^2x = \frac{1 – \cos 2x}{2} \cdot \frac{1 + \cos 2x}{2} = \frac{(1 – \cos 2x)(1 + \cos 2x)}{4}$.
$(1 – \cos 2x)(1 + \cos 2x) = 1 – \cos^2 2x$.
Thay $\cos^2 2x = \frac{1 + \cos 4x}{2}$:
$\sin^2x \cos^2x = \frac{1 – \frac{1 + \cos 4x}{2}}{4} = \frac{\frac{2 – 1 – \cos 4x}{2}}{4} = \frac{1 – \cos 4x}{8}$.
Vậy: $\sin^2x \cos^2x = \frac{1 – \cos 4x}{8}$.
Bài tập 3. Biến đổi $1 – 2\sin^2x$.
Lời giải
Thay $\sin^2x = \frac{1 – \cos 2x}{2}$:
$1 – 2\sin^2x = 1 – 2 \cdot \frac{1 – \cos 2x}{2} = 1 – (1 – \cos 2x) = 1 – 1 + \cos 2x = \cos 2x$.
Vậy: $1 – 2\sin^2x = \cos 2x$.
Bài tập 4. Biến đổi $2\cos^2x – 1$.
Lời giải
Thay $\cos^2x = \frac{1 + \cos 2x}{2}$:
$2\cos^2x – 1 = 2 \cdot \frac{1 + \cos 2x}{2} – 1 = 1 + \cos 2x – 1 = \cos 2x$.
Vậy: $2\cos^2x – 1 = \cos 2x$.
Bài tập 5. Biến đổi $\tan^2x$.
Lời giải
Áp dụng công thức: $\tan^2x = \frac{\sin^2x}{\cos^2x} = \frac{\frac{1 – \cos 2x}{2}}{\frac{1 + \cos 2x}{2}} = \frac{1 – \cos 2x}{1 + \cos 2x}$.
Vậy: $\tan^2x = \frac{1 – \cos 2x}{1 + \cos 2x}$.
Bài tập 6. Biến đổi $\sin^6x$.
Lời giải
$\sin^6x = (\sin^2x)^3$.
Thay $\sin^2x = \frac{1 – \cos 2x}{2}$:
$\sin^6x = \left(\frac{1 – \cos 2x}{2}\right)^3 = \frac{(1 – \cos 2x)^3}{8}$.
Mở rộng:
$(1 – \cos 2x)^3 = 1 – 3\cos 2x + 3\cos^2 2x – \cos^3 2x$.
Thay $\cos^2 2x = \frac{1 + \cos 4x}{2}$, để đơn giản ta dừng ở bước cơ bản:
$\sin^6x = \frac{1 – 3\cos 2x + 3\frac{1 + \cos 4x}{2} – \cos^3 2x}{8}$.
(Để chi tiết hơn cần mở rộng $\cos^3 2x$, nhưng đây là dạng cơ bản.)
Vậy: $\sin^6x = \frac{1 – 3\cos 2x + 3\frac{1 + \cos 4x}{2} – \cos^3 2x}{8}$.
Bài tập 7. Rút gọn và biến đổi $\sin^4x + \cos^4x + 2\sin^2x \cos^2x$.
Lời giải
Sử dụng công thức hạ bậc
$\sin^4x$, $\cos^4x$, và $\sin^2x \cos^2x$ bằng các công thức hạ bậc:
$\sin^4x = \left(\frac{1 – \cos 2x}{2}\right)^2 = \frac{(1 – \cos 2x)^2}{4} = \frac{1 – 2\cos 2x + \cos^2 2x}{4}$, với $\cos^2 2x = \frac{1 + \cos 4x}{2}$,
$\sin^4x = \frac{1 – 2\cos 2x + \frac{1 + \cos 4x}{2}}{4} = \frac{1 – 2\cos 2x + \frac{1}{2} + \frac{\cos 4x}{2}}{4} = \frac{\frac{2 – 4\cos 2x + 1 + \cos 4x}{2}}{4} = \frac{3 – 4\cos 2x + \cos 4x}{8}$.
$\cos^4x = \left(\frac{1 + \cos 2x}{2}\right)^2 = \frac{(1 + \cos 2x)^2}{4} = \frac{1 + 2\cos 2x + \cos^2 2x}{4}$, với $\cos^2 2x = \frac{1 + \cos 4x}{2}$,
$\cos^4x = \frac{1 + 2\cos 2x + \frac{1 + \cos 4x}{2}}{4} = \frac{1 + 2\cos 2x + \frac{1}{2} + \frac{\cos 4x}{2}}{4} = \frac{\frac{2 + 4\cos 2x + 1 + \cos 4x}{2}}{4} = \frac{3 + 4\cos 2x + \cos 4x}{8}$.
$\sin^2x \cos^2x = \frac{1 – \cos 2x}{2} \cdot \frac{1 + \cos 2x}{2} = \frac{(1 – \cos 2x)(1 + \cos 2x)}{4} = \frac{1 – \cos^2 2x}{4}$, với $\cos^2 2x = \frac{1 + \cos 4x}{2}$,
$\sin^2x \cos^2x = \frac{1 – \frac{1 + \cos 4x}{2}}{4} = \frac{\frac{2 – 1 – \cos 4x}{2}}{4} = \frac{1 – \cos 4x}{8}$.
Khi đó: $\sin^4x + \cos^4x + 2\sin^2x \cos^2x = \frac{3 – 4\cos 2x + \cos 4x}{8} + \frac{3 + 4\cos 2x + \cos 4x}{8} + 2 \cdot \frac{1 – \cos 4x}{8}$.
$= \frac{(3 – 4\cos 2x + \cos 4x) + (3 + 4\cos 2x + \cos 4x) + 2(1 – \cos 4x)}{8}$ = 1
Kết luận: $\sin^4x + \cos^4x + 2\sin^2x \cos^2x = 1$.
6. Câu hỏi thường gặp (FAQ)
Công thức hạ bậc của sin²x là: $\sin^2x = \frac{1 – \cos(2x)}{2}$
Để áp dụng hiệu quả, bạn nên nhận diện biểu thức có lũy thừa bậc hai của sin, rồi thay công thức này để giảm bậc. Phương pháp này thường dùng trong bài toán rút gọn biểu thức lượng giác hoặc tính tích phân lượng giác cơ bản.
Công thức cơ bản là: $\cos^2x = \frac{1 + \cos(2x)}{2}$
Công thức này giúp chuyển biểu thức có $\cos^2x$ về dạng có $\cos(2x)$, giúp việc rút gọn hoặc giải phương trình lượng giác trở nên dễ hơn.
Các bài tập thường xoay quanh việc biến đổi biểu thức có dạng $\sin^2x, \cos^2x, \sin^4x, \cos^4x$ thành biểu thức chứa $\cos(2x)$ hoặc $\cos(4x)$.
Ví dụ: $\sin^4x = \frac{3 – 4\cos(2x) + \cos(4x)}{8}$
Công thức hạ bậc giúp chuyển các phương trình có bậc cao về bậc thấp hơn, ví dụ: $\sin^2x = \frac{1 – \cos(2x)}{2} \Rightarrow \text{phương trình trở về dạng có } \cos(2x).$
Nhờ đó, phương trình trở nên đơn giản và dễ giải bằng công thức nhân đôi hoặc đổi biến
Mẹo đơn giản:
Với sin, ta trừ cos(2x) → $\sin^2x = \frac{1 – \cos(2x)}{2}$
Với cos, ta cộng cos(2x) → $\cos^2x = \frac{1 + \cos(2x)}{2}$
Chỉ cần nhớ “sin trừ – cos cộng” là bạn đã nắm vững quy tắc hạ bậc cơ bản.
7. Tổng kết
Công thức hạ bậc là cầu nối giữa các công thức lượng giác quan trọng, giúp đơn giản hóa biểu thức và rút gọn bài toán hiệu quả.
Hãy nhớ 4 công thức chính:
$ \sin^2x = \frac{1 – \cos2x}{2}, \quad \cos^2x = \frac{1 + \cos2x}{2}, \quad \tan^2x = \frac{1 – \cos2x}{1 + \cos2x}, \quad \cot^2x = \frac{1 + \cos2x}{1 – \cos2x}. $
Công thức hạ bậc lượng giác giúp đơn giản hóa biểu thức phức tạp, mang đến cách tiếp cận mới mẻ. Nắm vững chúng, bạn sẽ giải toán nhanh hơn và khám phá thêm nhiều điều thú vị. Hy vọng LuongGiac.org đã giúp bạn thành thạo các công thức này!
