Công thức nhân lượng giác là công thức đặc biệt trong lượng giác, giúp giải quyết hiệu quả các bài toán về góc và cạnh trong tam giác. Bài viết này sẽ giới thiệu chi tiết về các công thức cụ thể như công thức nhân đôi, công thức nhân ba, công thức nhân bốn, … , cùng ứng dụng thực tiễn trong giải bài tập. Qua ví dụ minh họa, bài tập luyện tập và lời giải chi tiết, bạn sẽ nắm vững kiến thức cần thiết. Hãy khám phá để nâng cao kỹ năng giải toán lượng giác ngay hôm nay!
1. Các công thức nhân lượng giác
Nói về công thức lượng giác thì có rất nhiều! Tránh lan man nên bài viết này, chúng ta chỉ nói tới các công thức nhân đôi, nhân ba và nhân bốn trong lượng giác.
Công thức nhân đôi lượng giác
Có 3 công thức quan trọng cần nhớ:
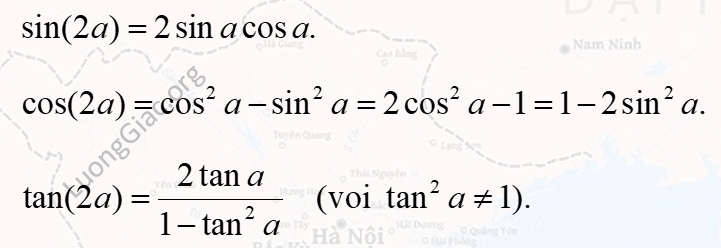
Công thức nhân ba lượng giác
Có 3 công thức quan trọng cần nhớ:
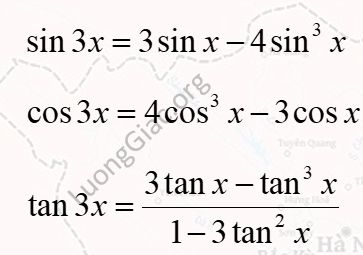
Công thức nhân bốn lượng giác
Có 2 công thức quan trọng cần nhớ:
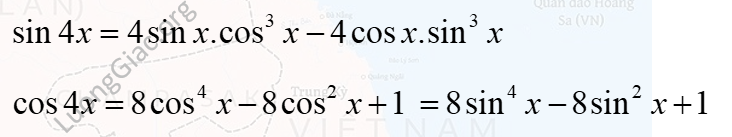
2. Bài tập vận dụng
Bài tập 1. Cho \(\sin \alpha = \frac{3}{5}\), với \(\alpha \in \left( \frac{\pi}{2}, \pi \right)\). Tính giá trị của \(\sin 2\alpha\) và \(\tan 2\alpha\).
Lời giải
Ta có \(\sin^2 \alpha + \cos^2 \alpha = 1 \Rightarrow \cos^2 \alpha = 1 – \sin^2 \alpha = \frac{16}{25}\).
Do \(\alpha \in \left( \frac{\pi}{2}, \pi \right)\) nên \(\cos \alpha < 0 \Rightarrow \cos \alpha = -\frac{4}{5}\).
$\sin 2\alpha = 2 \sin \alpha \cos \alpha = 2 \cdot \frac{3}{5} \cdot \left(-\frac{4}{5} \right) = \frac{-24}{25}.$
$\tan \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{3}{-4} = -\frac{3}{4} \Rightarrow \tan 2\alpha = \frac{2 \tan \alpha}{1 – \tan^2 \alpha} = \frac{2 \cdot \left(-\frac{3}{4} \right)}{1 – \left(-\frac{3}{4} \right)^2} = \frac{-6/4}{1 – 9/16} = \frac{-6/4}{7/16} = \frac{-24}{7}.$
Bài tập 2. Chứng minh các đẳng thức sau trong điều kiện có nghĩa của biểu thức
a) \(\sin^4 \alpha + \cos^4 \alpha = \frac{3}{4} + \frac{1}{4} \cos 4\alpha\)
b) \(\frac{1 – \cos \alpha + 2\cos 2\alpha}{\sin 2\alpha – \sin \alpha} = \cot \alpha\)
c) \(\frac{\sin^4 \alpha – \cos^4 \alpha + \cos^2 \alpha}{2(1 – \cos \alpha)} = \cos^2 \frac{\alpha}{2}\).
Lời giải
a) $VT = (\sin^2 \alpha + \cos^2 \alpha)^2 – 2\sin^2 \alpha \cos^2 \alpha = 1 – \frac{1}{2} \sin^2 2\alpha$
$= 1 – \frac{1 – \cos 4\alpha}{4} = \frac{3}{4} + \frac{1}{4} \cos 4\alpha = VP.$
b) $VT = \frac{1 – \cos \alpha + 2\cos^2 \alpha – 1}{2\sin \alpha \cos \alpha – \sin \alpha}= \frac{\cos \alpha (2\cos \alpha – 1)}{\sin \alpha (2\cos \alpha – 1)}= \frac{\cos \alpha}{\sin \alpha} = \cot \alpha = VP.$
c) $VT = \frac{\sin^4 \alpha + \cos^2 \alpha (1 – \cos^2 \alpha)}{2(1 – \cos \alpha)} = \frac{\sin^4 \alpha + \cos^2 \alpha \sin^2 \alpha}{2(1 – \cos \alpha)} = \frac{\sin^2 \alpha (\sin^2 \alpha + \cos^2 \alpha)}{2(1 – \cos \alpha)} $
$ = \frac{\sin^2 \alpha}{2(1 – \cos \alpha)} = \frac{1 – \cos^2 \alpha}{2(1 – \cos \alpha)} = \frac{1 + \cos 2\alpha}{2} = \frac{2\cos^2 \frac{\alpha}{2}}{2} = \cos^2 \frac{\alpha}{2} = VP. $
Bài tập 3. Cho biết \(\tan \frac{a}{2} = 2\). Hãy tính giá trị biểu thức: $P = \frac{\tan a + \cot a}{2\tan a – 4\cot a}.$
Lời giải
Ta có
$\tan a = \frac{2\tan \frac{a}{2}}{1 – \tan^2 \frac{a}{2}} = \frac{4}{3}, \quad \cot a = \frac{1}{\tan a} = \frac{3}{4}.$
$P = \frac{\frac{4}{3} – \frac{3}{4}}{2 \cdot \frac{4}{3} – 4 \cdot \frac{3}{4}} = \frac{-\frac{25}{12}}{\frac{8}{3} – 3} = \frac{-\frac{25}{12}}{\frac{1}{3}} = -\frac{25}{4}.$
Công thức nhân lượng giác là chìa khóa quan trọng để giải các bài toán lượng giác một cách nhanh chóng và chính xác. Việc nắm chắc kiến thức này không chỉ giúp bạn tự tin hơn khi làm bài tập mà còn mở ra nhiều cơ hội áp dụng vào thực tiễn. Hãy luyện tập thường xuyên để thành thạo và khám phá thêm các tài liệu liên quan nhằm nâng cao kiến thức lượng giác!
