1. Giới thiệu
Khi học về lượng giác, chúng ta thường bắt đầu với đường tròn lượng giác – nơi mọi giá trị của các hàm lượng giác được biểu diễn bằng vị trí điểm trên một vòng tròn đơn vị.
Từ nền tảng này, hai khái niệm cốt lõi xuất hiện: cung lượng giác và góc lượng giác.
Đây là hai cách khác nhau để mô tả mức độ quay của bán kính quanh tâm O của đường tròn lượng giác.
Nếu “đường tròn lượng giác” giúp chúng ta hình dung mối quan hệ giữa toạ độ điểm và giá trị các hàm sin, cos, thì “cung và góc lượng giác” lại giúp định lượng hóa chính xác sự quay đó – một bước không thể thiếu trước khi học đến các công thức lượng giác, đồng nhất thức, hay đồ thị hàm lượng giác.
2. Khái niệm cung lượng giác
Cung lượng giác là một phần của đường tròn lượng giác được tạo thành bởi chuyển động quay của bán kính từ vị trí ban đầu (thường là trục Ox dương) đến một vị trí xác định khác.
Ta gọi:
- Điểm đầu: $M_0(1, 0)$ – vị trí ban đầu trên trục Ox.
- Điểm cuối: $M(x, y)$ – vị trí sau khi quay một góc nhất định quanh tâm O.
- Chiều quay:
- Quay ngược chiều kim đồng hồ là chiều dương.
- Quay theo chiều kim đồng hồ là chiều âm.
👉 Như vậy, mỗi cung lượng giác tương ứng với một góc quay, có thể lớn hơn $360^\circ$ hoặc nhỏ hơn $0^\circ$, tùy thuộc số vòng quay.
Ví dụ: Cung đi từ $M_0$ đến $M$ khi quay $60^\circ$ ngược chiều kim đồng hồ gọi là cung dương có số đo $60^\circ$.
Nếu quay $-90^\circ$, tức là theo chiều kim đồng hồ, ta có cung âm $-90^\circ$.
Mỗi góc lượng giác đều ứng với một điểm duy nhất trên đường tròn. Để hiểu rõ cách xác định điểm này dựa vào giá trị góc, bạn hãy đọc thêm bài viết: Xác định điểm trên đường tròn lượng giác.
3. Số đo của cung lượng giác
Cung lượng giác có thể được đo bằng độ hoặc radian.
3.1. Số đo theo độ
Một vòng tròn hoàn chỉnh ứng với:
$360^\circ = 2\pi \text{ rad}$
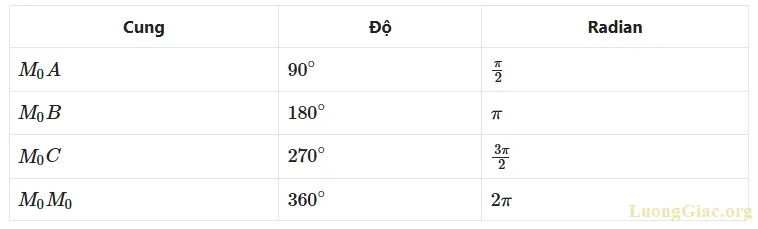
Các giá trị thường dùng:
3.2. Mối liên hệ giữa độ và radian
Công thức chuyển đổi rất quan trọng: $\frac{\alpha}{180^\circ} = \frac{l}{r\pi}$
Hay viết gọn: $1 \text{ rad} = \frac{180^\circ}{\pi} \quad \text{và} \quad 1^\circ = \frac{\pi}{180} \text{ rad}$
Ví dụ:
- $60^\circ = \frac{\pi}{3}$ rad
- $90^\circ = \frac{\pi}{2}$ rad
- $180^\circ = \pi$ rad
4. Góc lượng giác
Góc lượng giác là đại lượng đặc trưng cho mức độ quay của tia ban đầu đến tia cuối quanh một tâm cố định (thường là gốc toạ độ O).
4.1. Đặc điểm
- Góc lượng giác dương: quay ngược chiều kim đồng hồ.
- Góc lượng giác âm: quay theo chiều kim đồng hồ.
- Số đo của góc lượng giác có thể lớn hơn $2\pi$ hoặc nhỏ hơn $0$, vì bán kính có thể quay nhiều vòng.
4.2. Biểu diễn bằng đường tròn lượng giác
Trên đường tròn lượng giác, ta có:
- Mỗi góc lượng giác tương ứng với một điểm M(x, y).
- Tập hợp tất cả các điểm M ứng với các giá trị góc $\alpha$ tạo nên chu kỳ của hàm lượng giác.
Ví dụ:
- Với $\alpha = 0$, $M(1, 0)$
- Với $\alpha = \frac{\pi}{2}$, $M(0, 1)$
- Với $\alpha = \pi$, $M(-1, 0)$
- Với $\alpha = \frac{3\pi}{2}$, $M(0, -1)$
5. Mối quan hệ giữa cung và góc lượng giác
Cung lượng giác và góc lượng giác mô tả cùng một hiện tượng hình học — sự quay của một bán kính quanh tâm O.
Điểm khác nhau chỉ nằm ở cách biểu diễn:
| Tiêu chí | Cung lượng giác | Góc lượng giác |
|---|---|---|
| Hình học | Phần của đường tròn | Độ quay của bán kính |
| Đơn vị đo | Độ hoặc radian | Độ hoặc radian |
| Ứng dụng | Tính độ dài, cung tròn | Tính góc trong lượng giác |
Như vậy, ta có thể coi cung lượng giác và góc lượng giác là hai cách diễn đạt tương đương của cùng một đại lượng quay.
6. Cung lượng giác cùng phương, đối phương, bù nhau
6.1. Cung lượng giác cùng phương
Hai cung lượng giác cùng phương nếu có tia đầu và tia cuối cùng hướng.
Ví dụ: $\alpha = \frac{\pi}{6} \text{ và } \beta = \frac{13\pi}{6}$
Hai cung này cùng phương vì $\beta – \alpha = 2\pi$.
6.2. Cung lượng giác đối phương
Hai cung được gọi là đối phương nếu tia cuối của cung này là tia đối của tia cuối cung kia.
Ví dụ: $\alpha = \frac{\pi}{4} \text{ và } \beta = \frac{5\pi}{4}$
6.3. Cung lượng giác bù nhau
Hai cung bù nhau nếu tổng số đo bằng $\pi$: $ \alpha + \beta = \pi $
Ví dụ: $ \alpha = \frac{\pi}{3}, \beta = \frac{2\pi}{3} $
7. Mối liên hệ giữa cung, góc và giá trị lượng giác
Trên đường tròn lượng giác:
- Hoành độ của điểm M(x, y) biểu thị giá trị $\cos\alpha$.
- Tung độ của điểm M(x, y) biểu thị giá trị $\sin\alpha$.
Do đó: $ \cos\alpha = x \quad \text{và} \quad \sin\alpha = y $
Đây chính là mối liên hệ nền tảng giữa hình học (điểm trên đường tròn) và đại số (giá trị lượng giác), mở đường cho việc xây dựng các công thức như: $ \sin^2\alpha + \cos^2\alpha = 1 $
8. Ứng dụng thực tế
Cung và góc lượng giác không chỉ là khái niệm lý thuyết. Chúng được dùng trong:
- Định vị góc quay trong cơ học và robot học.
- Tính toán chuyển động tròn trong vật lý.
- Đồ hoạ máy tính, khi mô phỏng chuyển động quay.
Ví dụ: Một cánh quạt quay 5 vòng mỗi giây → số đo cung lượng giác mỗi giây là: $ 5 \times 2\pi = 10\pi \text{ rad} $
9. Kết luận
“Cung lượng giác và góc lượng giác” là nền tảng cho mọi phép tính lượng giác sau này.
Việc hiểu sâu hai khái niệm này giúp bạn:
- Dễ dàng chuyển đổi giữa độ – radian.
- Hiểu ý nghĩa hình học của các hàm sin, cos, tan.
- Và quan trọng nhất: nhận biết sự tuần hoàn và tính đối xứng trong lượng giác.