Dấu của các giá trị lượng giác

Trong lượng giác, không chỉ việc tính giá trị sin, cos, tan, cot quan trọng mà dấu của chúng (dương hay âm) cũng là yếu tố quyết định trong nhiều bài toán. Khi một góc thay đổi vị trí trên đường tròn lượng giác, dấu của các giá trị lượng giác sẽ thay đổi theo từng góc phần tư.

Hiểu được quy tắc này giúp bạn xác định chính xác giá trị lượng giác của mọi góc mà không cần phải thuộc lòng bảng giá trị phức tạp.

1. Ôn tập nhanh

Trên đường tròn lượng giác, mỗi góc $\alpha$ tương ứng với một điểm $M(x, y)$. Khi đó, ta định nghĩa:

$\sin \alpha = y, \quad \cos \alpha = x, \quad \tan \alpha = \frac{y}{x}, \quad \cot \alpha = \frac{x}{y}$

Như vậy, dấu của các giá trị lượng giác phụ thuộc trực tiếp vào dấu của $x$ và $y$ tại vị trí điểm $M$ trên mặt phẳng tọa độ.

👉 Nếu bạn chưa nắm vững khái niệm này, nên đọc trước bài: Giá trị lượng giác của một góc để hiểu rõ mối quan hệ giữa góc và tọa độ điểm.

2. Mặt phẳng tọa độ và 4 góc phần tư

Mặt phẳng tọa độ được chia làm 4 góc phần tư:

Góc phần tư	Khoảng góc (độ)	Dấu x	Dấu y
I	$0° < \alpha < 90°$	+	+
II	$90° < \alpha < 180°$	–	+
III	$180° < \alpha < 270°$	–	–
IV	$270° < \alpha < 360°$	+	–

Dấu của $x$ và $y$ chính là cơ sở để xác định dấu của các giá trị lượng giác tương ứng.

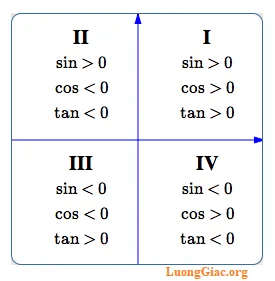
3. Dấu của các giá trị lượng giác trong từng góc phần tư

Góc phần tư thứ nhất

Ở góc phần tư thứ nhất, $x > 0$ và $y > 0$ nên:

$ \sin \alpha = y > 0, \quad \cos \alpha = x > 0 $

$ \tan \alpha = \frac{y}{x} > 0, \quad \cot \alpha = \frac{x}{y} > 0 $

➡ Kết luận: Tất cả các giá trị lượng giác đều dương.

Đây là góc phần tư “an toàn” nhất khi làm bài tập.

Góc phần tư thứ hai

Trong phần tư II: $x < 0, y > 0$, ta có:

$ \sin \alpha = y > 0, \quad \cos \alpha = x < 0 $

$ \tan \alpha = \frac{y}{x} < 0, \quad \cot \alpha = \frac{x}{y} < 0 $

➡ Kết luận: Chỉ sin và cosec là dương, còn lại đều âm.

Góc phần tư thứ ba

Ở phần tư III: $x < 0, y < 0$, nên:

$ \sin \alpha = y < 0, \quad \cos \alpha = x < 0 $

$ \tan \alpha = \frac{y}{x} > 0, \quad \cot \alpha = \frac{x}{y} > 0 $

➡ Kết luận: Tan và cot là dương, các giá trị khác âm.

Góc phần tư thứ tư

Trong phần tư IV: $x > 0, y < 0$, nên:

$ \sin \alpha = y < 0, \quad \cos \alpha = x > 0 $

$ \tan \alpha = \frac{y}{x} < 0, \quad \cot \alpha = \frac{x}{y} < 0 $

➡ Kết luận: Cos và sec là dương, còn lại âm.

Bảng tổng hợp dấu lượng giác

Ngoài ra, việc ghi nhớ các giá trị lượng giác đặc biệt sẽ giúp bạn kiểm tra nhanh kết quả tính toán và phát hiện sai dấu kịp thời. Bạn có thể tra cứu trong Bảng giá trị lượng giác đặc biệt (0°, 30°, 45°, 60°, 90°) . Còn muốn củng cố kỹ năng, hãy luyện tập qua các dạng bài trong Giải bài tập tính giá trị lượng giác – nơi bạn có thể vận dụng lý thuyết về dấu để xử lý các bài toán thực tế một cách hiệu quả.

4. Dấu của giá trị lượng giác tại các vị trí đặc biệt

Tại trục hoành (Ox)

• $\alpha = 0°$ hoặc $360°$: $\sin \alpha = 0, \quad \cos \alpha = 1$
• $\alpha = 180°$: $\sin \alpha = 0, \quad \cos \alpha = -1$

Tại trục tung (Oy)

• $\alpha = 90°$: $\sin \alpha = 1, \quad \cos \alpha = 0$
• $\alpha = 270°$: $\sin \alpha = -1, \quad \cos \alpha = 0$

Khi $\cos \alpha = 0$ thì $\tan \alpha$ không xác định vì mẫu bằng 0.

Để nắm vững bản chất, bạn nên bắt đầu từ bài viết Giá trị lượng giác của một góc, nơi trình bày rõ mối quan hệ giữa góc và các hàm lượng giác cơ bản. Sau đó, hãy tìm hiểu thêm cách tính giá trị lượng giác của một cung trong bài Tính giá trị lượng giác của một cung, để hiểu được vì sao cùng một cung nhưng giá trị lượng giác lại có thể mang dấu khác nhau.

5. Ví dụ minh họa

Ví dụ 1: Tính dấu của các giá trị lượng giác khi $\alpha = 120°$.

Góc $120°$ nằm ở phần tư II → sin dương, còn lại âm.

$ \sin 120° = \sin 60° = \frac{\sqrt{3}}{2} > 0 $

$ \cos 120° = -\cos 60° = -\frac{1}{2} $

$ \tan 120° = -\tan 60° = -\sqrt{3} $

Ví dụ 2: Tính dấu của các giá trị lượng giác khi $\alpha = 210°$.

Góc $210°$ thuộc phần tư III → tan, cot dương.

$ \sin 210° = -\sin 30° = -\frac{1}{2} $

$ \cos 210° = -\cos 30° = -\frac{\sqrt{3}}{2} $

$ \tan 210° = \tan 30° = \frac{1}{\sqrt{3}} > 0 $

Ví dụ 3: Tính dấu của các giá trị lượng giác khi $\alpha = 330°$.

Góc $330°$ nằm phần tư IV → cos dương.

$ \sin 330° = -\sin 30° = -\frac{1}{2} $

$ \cos 330° = \cos 30° = \frac{\sqrt{3}}{2} $

$ \tan 330° = -\tan 30° = -\frac{1}{\sqrt{3}} $

6. Dấu lượng giác khi góc lớn hơn 360° hoặc âm

Với góc lớn hơn 360°

Dấu không thay đổi vì tính chu kỳ của hàm lượng giác:

$\sin(\alpha + 360°) = \sin \alpha, \quad \cos(\alpha + 360°) = \cos \alpha$

Tức là chỉ cần lấy phần dư của góc sau khi chia cho 360°.

Với góc âm

Góc âm đối xứng qua trục hoành nên:

$\sin(-\alpha) = -\sin \alpha, \quad \cos(-\alpha) = \cos \alpha$

$\tan(-\alpha) = -\tan \alpha, \quad \cot(-\alpha) = -\cot \alpha$

7. Dấu lượng giác theo công thức góc đặc biệt

Dựa trên các công thức biến đổi:

• $\sin(180° + \alpha) = -\sin \alpha$
• $\cos(180° + \alpha) = -\cos \alpha$
• $\sin(360° – \alpha) = -\sin \alpha$
• $\cos(360° – \alpha) = \cos \alpha$

Những công thức này giúp xác định dấu nhanh mà không cần nhớ từng phần tư cụ thể.

8. FAQs

9. Kết luận

Việc xác định dấu của các giá trị lượng giác giúp tránh sai sót khi tính toán sin, cos, tan trong các góc khác nhau.

Chỉ cần ghi nhớ quy tắc: “Tất cả – Sin – Tang – Cos”

và hiểu ý nghĩa của từng góc phần tư, bạn có thể nhanh chóng xác định đúng dấu của bất kỳ giá trị lượng giác nào.