Trong lượng giác, việc hiểu rõ giá trị lượng giác của một góc là nền tảng để ta tính toán, chứng minh, và ứng dụng vào các bài toán hình học, dao động hay sóng cơ. Từ khái niệm cơ bản trên đường tròn lượng giác, ta có thể định nghĩa được sáu giá trị lượng giác quen thuộc: sin, cos, tan, cot, sec và cosec — mỗi giá trị đều mang một ý nghĩa hình học cụ thể và gắn với vị trí của góc trên mặt phẳng tọa độ.
1. Khái niệm về giá trị lượng giác của một góc
1.1 Góc và vị trí trên đường tròn lượng giác
Giả sử ta có đường tròn lượng giác tâm \( O(0, 0) \), bán kính bằng 1.
Trên đường tròn này, điểm \( M(x, y) \) biểu diễn góc lượng giác \( \alpha \), được đo ngược chiều kim đồng hồ từ trục hoành dương \( Ox \).
Như vậy, mỗi góc tương ứng với một điểm duy nhất trên đường tròn lượng giác, và ngược lại.
Từ đây, tọa độ của điểm ( M ) sẽ quyết định giá trị lượng giác của góc \( \alpha \).
1.2 Sáu giá trị lượng giác cơ bản
Giá trị lượng giác của góc \( \alpha \) được định nghĩa dựa trên tọa độ \( (x, y) \) của điểm \( M \) trên đường tròn lượng giác như sau:
$ \sin \alpha = y, \quad \cos \alpha = x $
$ \tan \alpha = \frac{y}{x}, \quad \cot \alpha = \frac{x}{y} $
$ \sec \alpha = \frac{1}{x}, \quad \csc \alpha = \frac{1}{y} $
Trong đó:
- $\sin \alpha$ biểu thị tung độ của điểm \( M \).
- $\cos \alpha$ biểu thị hoành độ của điểm \( M \).
- $\tan \alpha$ và $\cot \alpha$ mô tả tỉ số giữa hai tọa độ.
- $\sec \alpha$ và $\csc \alpha$ là nghịch đảo của $\cos \alpha$ và $\sin \alpha$ tương ứng.
Lưu ý: Các giá trị $\tan \alpha$, $\cot \alpha$, $\sec \alpha$, $\csc \alpha$ chỉ xác định khi mẫu khác 0.
Ví dụ: $\tan \alpha$ không xác định khi $\cos \alpha = 0$ (tức $\alpha = 90^\circ + k180^\circ$).
2. Mối liên hệ giữa các giá trị lượng giác của một góc
Các giá trị lượng giác không tồn tại tách biệt mà liên kết chặt chẽ với nhau qua những đẳng thức cơ bản và mối quan hệ đối ngẫu.
2.1 Đẳng thức lượng giác cơ bản
Từ định nghĩa trên đường tròn lượng giác, ta luôn có: $ x^2 + y^2 = 1 $
Thay $x = \cos \alpha$, $y = \sin \alpha$, ta suy ra: $ \sin^2 \alpha + \cos^2 \alpha = 1 $
Từ đẳng thức này, ta có thể rút ra nhiều hệ thức tương đương:
$ 1 + \tan^2 \alpha = \frac{1}{\cos^2 \alpha} $
$ 1 + \cot^2 \alpha = \frac{1}{\sin^2 \alpha} $
Những công thức này là nền tảng cho nhiều phép biến đổi trong giải phương trình lượng giác và chứng minh đẳng thức.
2.2 Mối quan hệ đối ngẫu giữa các giá trị lượng giác
Các giá trị lượng giác của hai góc phụ nhau (tổng bằng (90^\circ)) có liên hệ đối ngẫu rất thú vị:
$ \sin \alpha = \cos (90^\circ – \alpha) $
$ \tan \alpha = \cot (90^\circ – \alpha) $
$ \sec \alpha = \csc (90^\circ – \alpha) $
Nhờ mối quan hệ này, khi biết một giá trị lượng giác, ta có thể dễ dàng suy ra giá trị của giá trị đối ngẫu tương ứng.
Các mối quan hệ này sẽ được khai thác chi tiết trong bài “Dấu của các giá trị lượng giác trong bốn góc phần tư”.
3. Liên hệ giữa giá trị lượng giác của góc và cung lượng giác
Khi làm việc trên đường tròn lượng giác, một cung và một góc có cùng điểm cuối sẽ có cùng giá trị lượng giác.
Điều này cho phép ta tính giá trị lượng giác của một cung dựa vào giá trị của góc tương ứng.
Ví dụ: $\sin l = \sin \alpha, \quad \cos l = \cos \alpha$
Do đó, giá trị lượng giác không chỉ phụ thuộc vào độ lớn của góc mà còn vào vị trí điểm cuối trên đường tròn lượng giác.
4. Các giá trị lượng giác đặc biệt thường gặp
Trong học tập và thi cử, ta thường gặp các góc có giá trị đặc biệt, giúp việc tính toán trở nên dễ dàng hơn.
Các góc tiêu biểu bao gồm: \(0^\circ\), \(30^\circ\), \(45^\circ\), \(60^\circ\), \(90^\circ\).
Ví dụ:
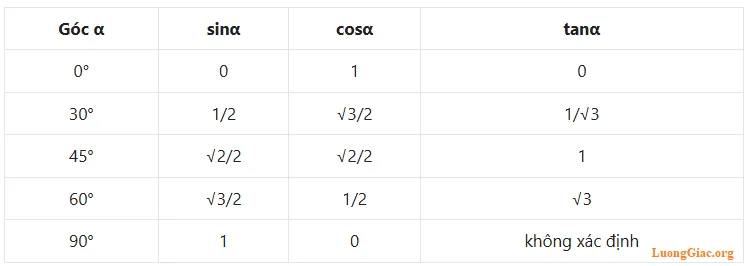
Có thể tìm hiểu chi tiết hơn về bảng giá trị lượng giác đặc biệt
5. Dấu của các giá trị lượng giác theo góc phần tư
Trên đường tròn lượng giác, tùy vào vị trí của góc ( \alpha ), dấu của các giá trị sin, cos, tan sẽ thay đổi theo bốn góc phần tư.
| Góc phần tư | Dấu của sin | Dấu của cos | Dấu của tan |
|---|---|---|---|
| I (0°–90°) | + | + | + |
| II (90°–180°) | + | – | – |
| III (180°–270°) | – | – | + |
| IV (270°–360°) | – | + | – |
6. Ứng dụng của giá trị lượng giác trong thực tế
Giá trị lượng giác không chỉ phục vụ trong hình học, mà còn được ứng dụng trong nhiều lĩnh vực khác nhau:
Vật lý: Biểu diễn dao động điều hòa, chuyển động tròn, sóng cơ học: $y = A\sin(\omega t + \varphi)$
Kỹ thuật: Tính toán góc nghiêng, chiều cao công trình, tầm nhìn, quỹ đạo.
Tin học và lập trình:
Dùng trong đồ họa máy tính, xoay vật thể 2D–3D, lập trình game.
Các giá trị $\sin$, $\cos$, $\tan$ giúp chuyển đổi giữa góc và độ dài, là cầu nối giữa đại số và hình học.
Tổng kết
Hiểu giá trị lượng giác của một góc chính là bước khởi đầu trong hành trình chinh phục các bài tập tính giá trị lượng giác. Khi nắm vững ý nghĩa hình học, công thức cơ bản và mối liên hệ giữa các giá trị, bạn có thể dễ dàng mở rộng sang các khái niệm cao hơn như cung lượng giác, biểu đồ sin-cos, hay ứng dụng trong vật lý sóng và dao động.