Trong chương trình lượng giác, sau khi học công thức nhân đôi (2x), nhiều học sinh bắt đầu gặp các biểu thức có dạng sin(3x), cos(3x) hoặc tan(3x). Đây chính là lúc công thức nhân ba (3x) phát huy tác dụng — giúp ta biến đổi các biểu thức bậc cao về dạng cơ bản của sin, cos, tan.
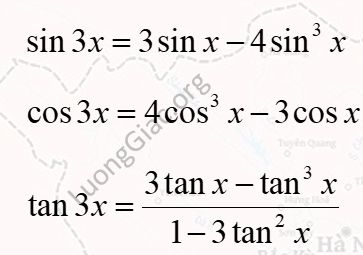
Hiểu rõ công thức này không chỉ giúp rút gọn và chứng minh đẳng thức lượng giác, mà còn mở đường cho việc học các công thức biến đổi phức tạp hơn sau này.
1. Ôn lại công thức nhân đôi
Công thức nhân ba là công thức nâng cao của công thức nhân lượng giác, được hình thành dựa trên công thức nhân đôi và công thức cộng lượng giác.
Trước hết, hãy nhắc lại các công thức cơ bản:
$\sin(2x) = 2\sin x \cos x$
$\cos(2x) = \cos^2 x – \sin^2 x$
$\tan(2x) = \frac{2\tan x}{1 – \tan^2 x}$
Từ các biểu thức trên, ta có thể thay ( 2x = (x + x) ) hoặc ( 3x = (2x + x) ) để xây dựng công thức nhân ba. Cách này giúp người học hiểu công thức không chỉ là “học thuộc” mà là “suy ra có logic”.
2. Công thức nhân ba (3x)
Công thức sin(3x)
Dựa vào công thức cộng: $\sin(3x) = \sin(2x + x) = \sin(2x)\cos x + \cos(2x)\sin x$
Thay công thức nhân đôi vào: $\sin(3x) = (2\sin x \cos x)\cos x + (\cos^2 x – \sin^2 x)\sin x$
Rút gọn: $\sin(3x) = 3\sin x – 4\sin^3 x$
➡️ Công thức chính: $\sin(3x) = 3\sin x – 4\sin^3 x$
Công thức cos(3x)
Tương tự, ta có: $\cos(3x) = \cos(2x + x) = \cos(2x)\cos x – \sin(2x)\sin x$
Thay công thức nhân đôi: $\cos(3x) = (\cos^2 x – \sin^2 x)\cos x – (2\sin x \cos x)\sin x$
Rút gọn biểu thức: $\cos(3x) = 4\cos^3 x – 3\cos x$
➡️ Công thức chính: $\cos(3x) = 4\cos^3 x – 3\cos x$
Công thức tan(3x)
Bắt đầu từ công thức cộng tang: $\tan(3x) = \tan(2x + x) = \frac{\tan 2x + \tan x}{1 – \tan 2x \tan x}$
Thay công thức nhân đôi của tang vào: $\tan(2x) = \frac{2\tan x}{1 – \tan^2 x}$
Sau một vài bước rút gọn, ta được: $\tan(3x) = \frac{3\tan x – \tan^3 x}{1 – 3\tan^2 x}$
➡️ Công thức chính: $\tan(3x) = \frac{3\tan x – \tan^3 x}{1 – 3\tan^2 x}$
3. So sánh nhanh: Nhân đôi và nhân ba
| Dạng công thức | Biểu thức | Đặc điểm |
|---|---|---|
| Nhân đôi (2x) | $\sin(2x) = 2\sin x \cos x$ | Tăng bậc 2 |
| Nhân ba (3x) | $\sin(3x) = 3\sin x – 4\sin^3 x$ | Tăng bậc 3 |
| Tác dụng | Biến đổi, rút gọn, chứng minh | Tạo nền cho các công thức cao hơn |
Nhận xét: công thức nhân ba có dạng đa thức bậc ba theo sin, cos, tan. Khi học lên cao, bạn sẽ gặp các công thức nhân bốn, nhân năm – chúng đều được mở rộng từ mô hình này.
4. Bảng tổng hợp công thức nhân ba
| Hàm lượng giác | Biểu thức chính | Ghi nhớ nhanh |
|---|---|---|
| $\sin(3x)$ | $3\sin x – 4\sin^3 x$ | “3 trừ 4 sin³x” |
| $\cos(3x)$ | $4\cos^3 x – 3\cos x$ | “4 cos³x trừ 3 cosx” |
| $\tan(3x)$ | $\frac{3\tan x – \tan^3 x}{1 – 3\tan^2 x}$ | “Bậc 3 của tan” |
5. Bài tập vận dụng
Bài tập 1: Cho \( \tan(a) = 2 \). Tính giá trị của \( \sin(3a) \) và \( \cos(3a) \).
Lời giải
Sử dụng công thức nhân ba: $ \sin(3a) = 3\sin(a) – 4\sin^3(a) $ $ \cos(3a) = 4\cos^3(a) – 3\cos(a) $
Giải phương trình với giá trị đã cho:
Vì \( \tan(a) = 2 \), ta có \( \sin(a) = \frac{2}{\sqrt{5}} \) và \( \cos(a) = \frac{1}{\sqrt{5}} \).
Thay vào công thức: $ \sin(3a) = 3 \times \frac{2}{\sqrt{5}} – 4 \times \left(\frac{2}{\sqrt{5}}\right)^3 = \frac{6}{\sqrt{5}} – \frac{32}{5\sqrt{5}} = \frac{6 – 32/5}{\sqrt{5}} = \frac{-2}{\sqrt{5}} $ $ \cos(3a) = 4 \times \left(\frac{1}{\sqrt{5}}\right)^3 – 3 \times \frac{1}{\sqrt{5}} = \frac{4}{5\sqrt{5}} – \frac{3}{\sqrt{5}} = \frac{4 – 15}{5\sqrt{5}} = \frac{-11}{5\sqrt{5}} $
Bài tập 2: Tính tan(3x) biết tanx = 1
Lời giải
tan(3x) = (3tanx – tan³x)/(1 – 3tan²x)
= (3×1 – 1³)/(1 – 3×1²)
= (3 – 1)/(1 –3)
= 2/(-2) = -1
Bài tập 3: Rút gọn biểu thức: A = cos(3x) + cos(x)
Lời giải
Sử dụng công thức cos(3x) = 4cos³(x) – 3cos(x):
A = (4cos³(x) – 3cos(x)) + cos(x)
A = 4cos³(x) – 2cos(x)
A = 2cos(x)(2cos²(x) – 1)
Chúng ta biết 2cos²(x) – 1 = cos(2x), vậy:
A = 2cos(x)cos(2x)
Bài tập 4: Cho cosx = 1/2. Tính cos(3x)
Lời giải
cos(3x) = 4cos³x – 3cosx
= 4(1/2)³ – 3(1/2)
= 4(1/8) – 3/2
= 1/2 – 3/2
= -1
Bài tập 5: Giải phương trình: tan(3x) = tan(x)
Lời giải
Điều kiện xác định: x ≠ π/2 + kπ, x ≠ π/6 + kπ/2, x ≠ 5π/6 + kπ/2 (để tan(x), tan(3x) có nghĩa).
Từ tan(3x) = tan(x), ta có:
3x = x + kπ
2x = kπ
x = kπ/2, với k là số nguyên.
Tuy nhiên, chúng ta cần kiểm tra lại điều kiện xác định.
Nếu x = kπ/2, các trường hợp có thể xảy ra:
k chẵn (k=2m): x = mπ. tan(mπ) = 0, tan(3mπ) = 0. Thỏa mãn.
k lẻ (k=2m+1): x = (2m+1)π/2. Lúc này cos(x) = 0, nên tan(x) không xác định. Loại.
Vậy nghiệm của phương trình là x = kπ, với k là số nguyên.
Ví dụ này nhấn mạnh tầm quan trọng của việc xem xét điều kiện xác định khi sử dụng các công thức lượng giác, đặc biệt là với hàm tang.
Bài tập 6: Tính giá trị của sin(3x) biết sinx = 1/2
Lời giải
Áp dụng công thức:
sin(3x) = 3sinx – 4sin³x
= 3(1/2) – 4(1/2)³
= 3/2 – 4(1/8)
= 3/2 – 1/2
= 1
Bài tập 7: Chứng minh đẳng thức: (sin(3x) + sin(x)) / (cos(3x) + cos(x)) = tan(2x)
Lời giải
Chúng ta sẽ biến đổi vế trái:
Tử số: sin(3x) + sin(x) = (3sin(x) – 4sin³(x)) + sin(x) = 4sin(x) – 4sin³(x) = 4sin(x)(1 – sin²(x)) = 4sin(x)cos²(x)
Mẫu số: cos(3x) + cos(x) = (4cos³(x) – 3cos(x)) + cos(x) = 4cos³(x) – 2cos(x) = 2cos(x)(2cos²(x) – 1) = 2cos(x)cos(2x)
Vậy, vế trái trở thành:
[4sin(x)cos²(x)] / [2cos(x)cos(2x)]
Điều kiện: cos(x) ≠ 0 và cos(2x) ≠ 0.
Nếu cos(x) ≠ 0, ta có thể rút gọn cos(x):
= [4sin(x)cos(x)] / [2cos(2x)]
Ta biết 2sin(x)cos(x) = sin(2x). Vậy:
= [2sin(2x)] / [2cos(2x)]
= sin(2x) / cos(2x)
= tan(2x)
Bài 8. Chứng minh rằng: $\cos(3x) = 4\cos^3 x – 3\cos x$
Gợi ý: Dùng công thức cộng cos(2x + x) và biến đổi tương tự phần chứng minh trên.
Bài 9. Tính $\tan(3x)$ khi $\tan x = \frac{1}{2}$.
$\tan(3x) = \frac{3\tan x – \tan^3 x}{1 – 3\tan^2 x} = \frac{3\left(\frac{1}{2}\right) – \left(\frac{1}{2}\right)^3}{1 – 3\left(\frac{1}{2}\right)^2} = \frac{\frac{11}{8}}{\frac{1}{4}} = \frac{11}{2}$
Bài 10. Rút gọn: $\sin(3x) + \sin x$
→ Sử dụng công thức tổng thành tích để đưa về dạng tích của sin và cos.
6. Kết luận
Công thức nhân ba (3x) là bước mở rộng quan trọng trong hệ thống công thức lượng giác, giúp chuyển đổi các biểu thức bậc cao về dạng đơn giản hơn.
Việc hiểu rõ cách chứng minh, mối liên hệ và ứng dụng của công thức này không chỉ giúp bạn làm tốt bài tập mà còn củng cố nền tảng để học các công thức biến đổi phức tạp hơn như “tổng thành tích” hay “góc liên kết”.