Trong hệ thống các công thức nhân lượng giác, nhóm công thức nhân đôi đóng vai trò đặc biệt quan trọng. Đây là cầu nối giữa công thức cộng góc và công thức hạ bậc, giúp rút gọn biểu thức, giải phương trình, và tính nhanh giá trị các hàm lượng giác.
Nếu bạn đã nắm vững các công thức cơ bản, hãy cùng đi sâu vào cơ chế hình thành, chứng minh và ứng dụng của công thức nhân đôi — nền tảng cho các bài toán nâng cao trong lượng giác.
1. Khái niệm “Nhân đôi góc” là gì?
Trong lượng giác, nhân đôi góc có nghĩa là ta xem xét giá trị của các hàm lượng giác khi góc được nhân đôi, tức là thay vì $x$, ta xét $2x$.
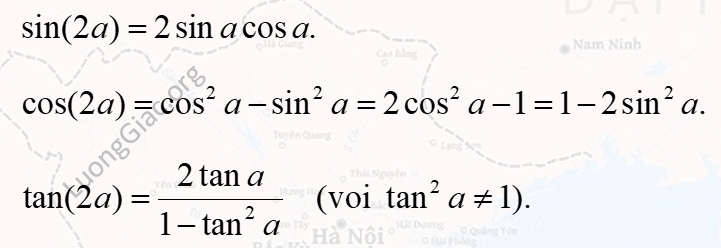
Ví dụ:
- Từ $\sin x$, ta xét $\sin 2x$
- Từ $\cos x$, ta xét $\cos 2x$
- Từ $\tan x$, ta xét $\tan 2x$
Điều thú vị là, nhờ các công thức nhân đôi, ta có thể biểu diễn các hàm của góc $2x$ hoàn toàn theo $\sin x$ và $\cos x$. Điều này giúp rút gọn các biểu thức phức tạp, hoặc hạ bậc phương trình về dạng đơn giản hơn.
2. Hệ thống công thức nhân đôi lượng giác
Dưới đây là ba công thức chuẩn bạn cần ghi nhớ:
$\sin 2x = 2\sin x \cos x$
$\cos 2x = \cos^2 x – \sin^2 x$
$\tan 2x = \frac{2\tan x}{1 – \tan^2 x}$
Trong đó, công thức của $\cos 2x$ có thể được viết lại dưới nhiều dạng tương đương:
- $\cos 2x = 1 – 2\sin^2 x$
- $\cos 2x = 2\cos^2 x – 1$
Việc lựa chọn dạng nào phụ thuộc vào dữ kiện đề bài. Nếu bài toán cho $\sin x$, bạn nên dùng dạng $1 – 2\sin^2 x$; còn nếu cho $\cos x$, thì $2\cos^2 x – 1$ sẽ tiện hơn.
3. Cách chứng minh
Từ công thức cộng, ta có:
$\sin (x + y) = \sin x \cos y + \cos x \sin y$
$\cos (x + y) = \cos x \cos y – \sin x \sin y$
Thay $y = x$, ta được:
- $\sin 2x = 2\sin x \cos x$
- $\cos 2x = \cos^2 x – \sin^2 x$
Với $\tan 2x$, ta có:
$\tan 2x = \frac{\tan x + \tan x}{1 – \tan x \tan x} = \frac{2\tan x}{1 – \tan^2 x}$
4. Mẹo ghi nhớ
Một cách học thuộc dễ nhớ được nhiều học sinh áp dụng:
| Hàm lượng giác | Công thức nhân đôi | Mẹo nhớ |
|---|---|---|
| $\sin 2x$ | $2\sin x \cos x$ | “Nhân 2 – sin cos song hành” |
| $\cos 2x$ | $1 – 2\sin^2 x$ hoặc $2\cos^2 x – 1$ | “Trừ bình hoặc nhân đôi cos” |
| $\tan 2x$ | $\frac{2\tan x}{1 – \tan^2 x}$ | “Phân thức đặc trưng tan” |
Ngoài ra, bạn có thể sử dụng sơ đồ tư duy hoặc infographic công thức lượng giác (sẽ có trong bài tổng hợp) để ghi nhớ lâu hơn.
5. Bài tập công thức nhân đôi
Bài tập 1: Tính $\sin 2x$, $\cos 2x$ khi $\tan x = \frac{1}{2}$
Lời giải
Ta có $\sin x = \frac{\tan x}{\sqrt{1 + \tan^2 x}} = \frac{1}{\sqrt{5}}$, $\cos x = \frac{2}{\sqrt{5}}$
⇒ $\sin 2x = 2\sin x \cos x = \frac{4}{5}$
⇒ $\cos 2x = \frac{3}{5}$
Bài tập 2: Chứng minh đẳng thức: $\cos^2 x – \sin^2 x = 1 – 2\sin^2 x$
Lời giải
Hai vế bằng nhau vì cùng biểu diễn $\cos 2x$.
Bài tập 3: Rút gọn biểu thức: $\sin^2 x + \sin 2x + \cos^2 x$
Lời giải
$= 1 + \sin 2x = 1 + 2\sin x \cos x$
Bài tập 4: Tìm giá trị lớn nhất, nhỏ nhất của hàm số: y = 4sinx.cos x + 1.
Lời giải
Ta có y = 4sin x.cos x + 1 = 2sin 2x + 1.
Vì –1 ≤ sin 2x ≤ 1 nên –2 ≤ 2sin 2x ≤ 2
Suy ra –1 ≤ 2sin 2x + 1 ≤ 3 hay –1 ≤ y ≤ 3.
Bài 5: Rút gọn biểu thức: $A = \frac{2\cos^2 2\alpha + \sqrt{3}\sin 4\alpha – 1}{2\sin^2 2\alpha + \sqrt{3}\sin 4\alpha – 1}.$
Lời giải
Ta có
$A = \frac{2\cos^2 2\alpha + \sqrt{3}\sin 4\alpha – 1}{2\sin^2 2\alpha + \sqrt{3}\sin 4\alpha – 1}$
$= \frac{\cos 4\alpha + \sqrt{3}\sin 4\alpha}{\sqrt{3}\sin 4\alpha – \cos 4\alpha}$
$= \frac{\frac{1}{2}\cos 4\alpha + \frac{\sqrt{3}}{2}\sin 4\alpha}{\frac{\sqrt{3}}{2}\sin 4\alpha – \frac{1}{2}\cos 4\alpha}$
$= \frac{\sin(4\alpha + 30^\circ)}{\sin(4\alpha – 30^\circ)}.$
6. Mối liên hệ với các công thức khác
Công thức nhân đôi không tồn tại độc lập, mà liên kết chặt chẽ với các nhóm công thức khác trong lượng giác:
| Liên kết | Ý nghĩa |
|---|---|
| 🔗 Công thức hạ bậc lượng giác | Dạng chia đôi góc ($x/2$) là “đảo ngược” của nhân đôi |
| 🔗 Công thức nhân ba (3x) | Mở rộng từ nhân đôi sang góc nhân ba |
| 🔗 Công thức biến đổi lượng giác | Kết hợp nhân đôi với các phép biến đổi tổng – tích |
Nhờ đó, bài này vừa giúp bạn củng cố nền tảng, vừa mở hướng sang các chủ đề kế tiếp trong hệ thống công thức lượng giác.
7. Tổng kết và ghi nhớ nhanh
| Hàm | Công thức | Gợi nhớ |
|---|---|---|
| $\sin 2x$ | $2\sin x \cos x$ | Nhân 2 – sin cos song hành |
| $\cos 2x$ | $1 – 2\sin^2 x$ / $2\cos^2 x – 1$ | Trừ bình / nhân đôi cos |
| $\tan 2x$ | $\frac{2\tan x}{1 – \tan^2 x}$ | Tan đặc trưng |
Tóm lại: Công thức nhân đôi giúp biến đổi biểu thức, rút gọn phương trình, và liên kết nhiều định lý lượng giác với nhau. Nắm vững nhóm công thức này, bạn sẽ dễ dàng học tiếp các phần chia đôi, nhân ba, biến đổi tổng – tích.