Vận dụng những công thức biến đổi lượng giác ở bài trước sẽ giúp bạn giải bài tập rút gọn biểu thức lượng giác phức tạp thành dạng đơn giản hơn. Nhờ đó, bạn không chỉ tiết kiệm thời gian mà còn hiểu rõ hơn bản chất bài toán. Hãy nắm vững các công thức này để tự tin giải quyết mọi bài toán lượng giác!
Bài tập 1. Tính giá trị biểu thức $A = \sin^2 10^\circ + \cos 70^\circ \cos 50^\circ$
Lời giải
Ta có
$A = {\sin ^2}{10^0} + \cos {70^0}\cos {50^0}$ $ = \frac{{1 – \cos {{20}^0}}}{2} + \frac{1}{2}[\cos {120^0} + \cos {20^0}{\rm{]}}$
$ = \frac{1}{2} – \frac{1}{2}\cos {20^0} + \frac{1}{2}\cos {120^0} + \frac{1}{2}\cos {20^0}$
$ = \frac{1}{2} + \frac{1}{2}\cos {120^0}$
$ = \frac{1}{2} – \frac{1}{4} = \frac{1}{4}$
Vậy $A = \sin^2 10^\circ + \cos 70^\circ \cos 50^\circ = \frac{1}{4}.$
Bài tập 2. Rút gọn các biểu thức sau đây:
a) $A = \frac{\cos 4a – \cos 2a}{\sin 4a – \sin 2a} $
b) $ B = \frac{\sin a – 2\sin 2a + \sin 3a}{\cos a – 2\cos 2a + \cos 3a} $
Lời giải
a) Ta có
$A = \frac{\cos 4a – \cos 2a}{\sin 4a – \sin 2a} = \frac{-2\sin 3a \sin a}{2\cos 3a \sin a} = \frac{-\sin 3a}{\cos 3a} = -\tan 3a.$
b) Ta có
$B = \frac{{\sin a – 2\sin 2a + \sin 3a}}{{\cos a – 2\cos 2a + \cos 3a}}$
$ = \frac{{(\sin 3a + \sin a) – 2\sin 2a}}{{(\cos 3a + \cos a) – 2\cos 2a}}$
$ = \frac{{2\sin 2a\cos a – 2\sin 2a}}{{2\cos 2a\cos a – 2\cos 2a}}$
$ = \frac{{2\sin 2a(\cos a – 1)}}{{2\cos 2a(\cos a – 1)}}$
$ = \frac{{\sin 2a}}{{\cos 2a}} = \tan 2a.$
Bài tập 3. Rút gọn biểu thức $A = 2\sin x (\cos x + \cos 3x + \cos 5x).$
Từ đó tính giá trị biểu thức $T = \cos \frac{\pi}{7} + \cos \frac{3\pi}{7} + \cos \frac{5\pi}{7}.$
Lời giải
Ta có A = 2sinx(cosx + cos3x + cos5x)
= 2sinxcosx + 2sinxcos3x + 2sinxcos5x
= sin2x + sin4x + sin(−2x) + sin6x + sin(−4x)
= sin2x + sin4x − sin2x + sin6x − sin4x
Như vậy, A = 2sinx(cosx + cos3x + cos5x) = sin6x.
Áp dụng kết quả trên, ta có
$ T = \cos \frac{\pi}{7} + \cos \frac{3\pi}{7} + \cos \frac{5\pi}{7} $
$ \Rightarrow T \cdot 2\sin \frac{\pi }{7}$
$ = 2\sin \frac{\pi }{7}\left( {\cos \frac{\pi }{7} + \cos \frac{{3\pi }}{7} + \cos \frac{{5\pi }}{7}} \right)$ $ = \sin \frac{{6\pi }}{7}$
Do $ \sin \frac{6\pi}{7} = \sin \left( \pi – \frac{\pi}{7} \right) = \sin \frac{\pi}{7} $
nên $ T \cdot 2 \sin \frac{\pi}{7} = \sin \frac{\pi}{7} \Rightarrow T = \frac{1}{2}. $
Bài 4. Tính giá trị các biểu thức sau đây:
a) \( A = \sin \frac{\pi}{12} \sin \frac{5\pi}{12} \)
b) \( B = \cos \frac{11\pi}{12} \cos \frac{5\pi}{12} \)
c) \( C = \cos \frac{\pi}{5} – \cos \frac{2\pi}{5} \)
Lời giải
a)$A = \sin \frac{\pi }{{12}}\sin \frac{{5\pi }}{{12}}$ $ = \frac{1}{2}\left[ {\cos \left( { – \frac{{4\pi }}{{12}}} \right) – \cos \frac{{6\pi }}{{12}}} \right]$
$ = \frac{1}{2}\left[ {\cos \frac{\pi }{3} – \cos \frac{\pi }{2}} \right]$ $ = \frac{1}{2}\left( {\frac{1}{2} – 0} \right) = \frac{1}{4}$
b) $B = \cos \frac{{11\pi }}{{12}}\cos \frac{{5\pi }}{{12}}$
$ = \frac{1}{2}\left( {\cos \frac{{6\pi }}{{12}} + \cos \frac{{16\pi }}{{12}}} \right)$ $ = \frac{1}{2}\left( {\cos \frac{\pi }{2} – \cos \frac{{4\pi }}{{12}}} \right)$
$ = \frac{1}{2}\left( {0 – \frac{1}{2}} \right) = – \frac{1}{4}.$
c)
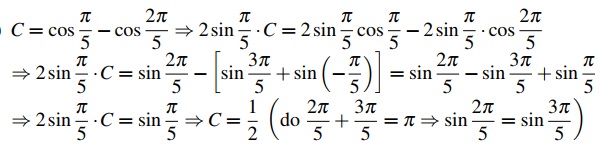
Rút gọn một biểu thức lượng giác là một dạng toán thường gặp trong phần lượng giác. Việc vận dụng các công thức biến đổi lượng giác sẽ biến những biểu thức phức tạp thành dạng đơn giản, dễ xử lý hơn. Muốn thành thạo, luyện tập thường xuyên là yếu tố không thể thiếu và quan trọng. Thực hành nhiều hơn nữa mỗi ngày không chỉ củng cố kiến thức lý thuyết mà còn rèn luyện phản xạ cũng như kỹ năng làm bài tập toán học tốt hơn.