Lượng giác không chỉ là một phần quan trọng của toán học mà còn có ứng dụng rộng rãi trong thực tế, từ kỹ thuật, thiên văn đến công nghệ. Trong đó, tính giá trị lượng giác của một cung giúp ta xác định \(\sin\), \(\cos\), \(\tan\),… của một góc, là nền tảng cho các bài toán lượng giác nâng cao. Hiểu rõ phần này giúp học sinh rèn tư duy logic, biến đổi biểu thức linh hoạt và ứng dụng hiệu quả. Hãy cùng khám phá chủ đề này để thấy toán học không chỉ lý thuyết mà còn đầy thú vị và hữu ích!
I. Tính giá trị lượng giác của một cung
Để tính giá trị lượng giác của 1 cung ta dựa vào các hằng đẳng thức lượng giác:
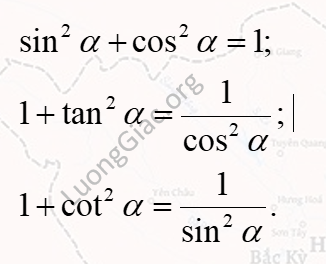
Ngoài ra, cần phải xác định dấu của các hàm số lượng giác của cung đó.
II. Bài tập
Bài tập 1. Biết \(\sin \alpha = \frac{1}{3}\) và \(\alpha \in \left(\frac{\pi}{2}; \pi \right)\). Tính giá trị của \(\cos \alpha\) và \(\tan \alpha\).
Lời giải
Do \(\alpha \in \left(\frac{\pi}{2}; \pi \right)\) nên \(\cos \alpha < 0\).
Mặt khác \(\sin^2 \alpha + \cos^2 \alpha = 1\) nên $ \cos^2 \alpha = 1 – \sin^2 \alpha = 1 – \frac{1}{9} = \frac{8}{9} \Rightarrow \cos \alpha = \pm \frac{2\sqrt{2}}{3}. $ (1)
Từ (1) và (2), suy ra \(\cos \alpha = -\frac{2\sqrt{2}}{3}\). (2)
Từ đó suy ra $ \tan \alpha = -\frac{1}{2\sqrt{2}}. $
Bài tập 2. Cho \(\cos \alpha = -\frac{12}{13}\) và \(\frac{\pi}{2} < \alpha < \pi\). Tính \(\sin \alpha\) và \(\tan \alpha\).
Lời giải
Ta có: $ \sin^2 \alpha = 1 – \cos^2 \alpha = 1 – \frac{144}{169} = \frac{25}{169} $
$ \Rightarrow \left[ {\begin{array}{{20}{l}} {\sin \alpha = \frac{5}{{13}}}\\ {\sin \alpha = – \frac{5}{{13}}} \end{array}} \right.$
Do \(\frac{\pi}{2} < \alpha < \pi\) nên \(\sin \alpha > 0\), do đó \(\sin \alpha = \frac{5}{13}\).
Từ đó ta có: $ \tan \alpha = -\frac{5}{12}. $
Bài tập 3. Cho \(\tan \alpha = -\frac{3}{4}\) ở đó \(\frac{\pi}{2} < \alpha < \pi\). Tính giá trị của \(\sin \alpha\).
Lời giải
Ta có $\frac{1}{\cos^2 \alpha} = 1 + \tan^2 \alpha = 1 + \frac{9}{16} = \frac{25}{16} \Rightarrow \cos^2 \alpha = \frac{16}{25}.$
Từ đó suy ra $ \sin^2 \alpha = 1 – \cos^2 \alpha = \frac{9}{25} \Rightarrow \sin \alpha = \pm \frac{3}{5}. $
Do \(\frac{\pi}{2} < \alpha < \pi\) nên \(\sin \alpha > 0\), do đó \(\sin \alpha = \frac{3}{5}\).
Bài tập 4. Cho \(\tan \alpha = 2\), tính giá trị biểu thức \(M = \cos^2 \alpha – \sin^2 \alpha\).
Lời giải
Ta có $ M = \frac{\cos^2 \alpha – \sin^2 \alpha}{\cos^2 \alpha + \sin^2 \alpha}. $
Chia cả tử và mẫu cho \(\cos^2 \alpha\), ta được $M = \frac{1 – \tan^2 \alpha}{1 + \tan^2 \alpha} \Rightarrow M = \frac{1 – 4}{1 + 4} = \frac{-3}{5}.$
Bài tập 5. Cho \(\cot \alpha = 3\). Tính giá trị biểu thức $ M = \frac{2\sin \alpha – 3\cos \alpha}{5\sin^3 \alpha + \cos^3 \alpha}. $
Lời giải
Ta có
$ M = \frac{2\sin \alpha – 3\cos \alpha}{5\sin^3 \alpha + \cos^3 \alpha} $ $ = \frac{2\left(\frac{1}{\sin^2 \alpha}\right) – 3\cot \alpha \left(\frac{1}{\sin^2 \alpha}\right)}{5 + \cot^3 \alpha} $ $ = \frac{-3\cot^3 \alpha + 2\cot^2 \alpha – 3\cot \alpha + 2}{5 + \cot^3 \alpha} $ $ = -\frac{35}{16}. $
Bài tập 6. Cho \(\frac{\pi}{2} < \alpha < \pi\) và \(\cos 2\alpha = -\frac{1}{9}\). Biết \(A = \sin 2\alpha + \cos 2\alpha = a + b\sqrt{5}\) với \(a, b \in \mathbb{Q}\) và \(\frac{a}{b} = \frac{p}{q}\) là phân số tối giản. Tính \(M = p – q\).
Lời giải
Do \(\frac{\pi}{2} < \alpha < \pi\) nên \(\pi < 2\alpha < 2\pi \Rightarrow \sin 2\alpha < 0\).
$\cos 2\alpha = -\frac{1}{9} \Rightarrow \sin^2 2\alpha = 1 – \cos^2 2\alpha = 1 – \frac{1}{81} = \frac{80}{81} \Rightarrow \sin 2\alpha = -\frac{4\sqrt{5}}{9}.$
Suy ra $ A = -\frac{1}{9} – \frac{4\sqrt{5}}{9}. $ $ \Rightarrow \begin{cases} a = -\frac{1}{9} \\ b = -\frac{4}{9} \end{cases} $ $ \Rightarrow \frac{a}{b} = \frac{1}{4} \Rightarrow p = 1, q = 4 \Rightarrow p – q = -3. $
Vậy \(M = -3\).
Bài tập 7. Cho \(\tan \alpha = \frac{1}{2}\), tính giá trị của biểu thức \(M = \frac{2\sin^2 \alpha + 3\sin \alpha \cos \alpha – 4\cos^2 \alpha}{5\cos^2 \alpha – \sin^2 \alpha}\).
Lời giải
Dễ thấy \(\cos \alpha \neq 0\), chia cả tử và mẫu của biểu thức \(M\) cho \(\cos^2 \alpha\) ta được:
$M = \frac{{2{{\tan }^2}\alpha + 3\tan \alpha – 4}}{{5 – {{\tan }^2}\alpha }}$ $ = \frac{{2 \cdot \frac{1}{4} + 3 \cdot \frac{1}{2} – 4}}{{5 – \frac{1}{4}}}$ $ = – \frac{8}{{19}}.$
Bài tập 8. Biết \(\sin \alpha + \cos \alpha = \frac{5}{4}\) và \(\sin \alpha > \cos \alpha\). Tính giá trị các biểu thức sau:
a) \(A = \sin \alpha \cdot \cos \alpha\).
b) \(B = \sin \alpha – \cos \alpha\).
Lời giải
a) Ta có $ \frac{25}{16} = (\sin \alpha + \cos \alpha)^2 = \sin^2 \alpha + \cos^2 \alpha + 2\sin \alpha \cdot \cos \alpha = 1 + 2\sin \alpha \cdot \cos \alpha. $
Từ đó suy ra $ 2A = \frac{9}{16} \Rightarrow A = \frac{9}{32}. $
b) Theo giả thiết ta có \(B > 0\) và $B^2 = \sin^2 \alpha + \cos^2 \alpha – 2\sin \alpha \cdot \cos \alpha = 1 – \frac{9}{16} = \frac{7}{16}.$
Từ đó suy ra $B = \frac{\sqrt{7}}{4}.$
Việc tính giá trị lượng giác của một cung không chỉ là bài toán kỹ thuật mà còn là bước nối giữa lý thuyết góc lượng giác và ứng dụng trong thực tế. Khi đã hiểu bản chất của cung lượng giác và các công thức chuyển đổi, bạn sẽ dễ dàng xác định được giá trị của các hàm $ \sin $, $ \cos $, $ \tan $ hay $ \cot $ trong mọi trường hợp.
Nếu bạn mới bắt đầu, hãy đọc lại bài Giá trị lượng giác của một góc để nắm rõ ý nghĩa và mối liên hệ giữa các hàm lượng giác. Điều này giúp bạn hiểu vì sao cùng một góc nhưng giá trị lượng giác có thể khác nhau khi xét trong đường tròn lượng giác.
Khi thực hành, bạn nên lưu ý đến dấu của các giá trị lượng giác trong 4 góc phần tư — một yếu tố dễ gây nhầm lẫn khi làm bài. Bài viết Dấu của các giá trị lượng giác sẽ giúp bạn phân biệt nhanh đâu là giá trị dương, đâu là giá trị âm tùy theo vị trí góc.
Ngoài ra, để tra cứu nhanh các giá trị đặc biệt như $30°$, $45°$, $60°$ hoặc $90°$, bạn có thể tham khảo Bảng giá trị lượng giác đặc biệt (0°, 30°, 45°, 60°, 90°). Cuối cùng, đừng quên luyện tập qua các dạng bài trong Giải bài tập tính giá trị lượng giác để củng cố kiến thức và tự tin khi làm các bài toán lượng giác phức tạp hơn.