1. Giới thiệu
Trong lượng giác, độ (°) và radian (rad) là hai đơn vị dùng để đo góc. Khi học các công thức sin, cos, tan hoặc tính toán trong vật lý, việc hiểu và biết chuyển đổi giữa độ và radian là bắt buộc.
Nhiều học sinh thường nhầm lẫn giữa hai đơn vị này, dẫn đến sai kết quả khi bấm máy tính hoặc làm bài tập. Bài viết này sẽ giúp bạn nắm chắc công thức, bảng chuyển đổi và cách sử dụng phù hợp — mà không trùng lặp nội dung với bài Góc lượng giác hay Độ dài cung lượng giác.
2. Khái niệm về độ và radian
2.1. Độ (Degree)
Độ là đơn vị đo góc quen thuộc nhất trong hình học phổ thông.
Một vòng tròn được chia thành 360 phần bằng nhau, mỗi phần tương ứng 1°.
Một số ví dụ cơ bản:
- Góc nhọn: nhỏ hơn 90°
- Góc vuông: 90°
- Góc bẹt: 180°
- Góc tròn: 360°
Đơn vị này trực quan, dễ hình dung nhưng không thuận tiện khi áp dụng vào công thức lượng giác hay giải tích.
2.2. Radian (Rad)
Radian được định nghĩa dựa trên tỷ số giữa độ dài cung tròn và bán kính của đường tròn.
$1\ \text{rad} = \frac{\text{độ dài cung tròn}}{\text{bán kính}}$
Nếu độ dài cung bằng bán kính, ta có góc 1 radian.
Vì chu vi đường tròn là $2\pi r$ nên một vòng tròn tương ứng: $2\pi\ \text{rad} = 360^\circ$
Từ đó, suy ra:
$1\ \text{rad} = \frac{180^\circ}{\pi} \approx 57,3^\circ$
$1^\circ = \frac{\pi}{180}\ \text{rad}$
Radian là đơn vị chuẩn trong các công thức toán học và vật lý hiện đại, vì nó liên hệ trực tiếp đến độ dài cung và các hàm sin, cos, tan.
3. Công thức chuyển đổi giữa độ và radian
3.1. Từ độ sang radian
Công thức: $\text{radian} = \text{độ} \times \frac{\pi}{180}$
Ví dụ: $60^\circ = 60 \times \frac{\pi}{180} = \frac{\pi}{3}\ \text{rad}$
3.2. Từ radian sang độ
Công thức: $\text{độ} = \text{radian} \times \frac{180}{\pi}$
Ví dụ: $\frac{\pi}{4}\ \text{rad} = \frac{\pi}{4} \times \frac{180}{\pi} = 45^\circ$
4. Bảng chuyển đổi độ ↔ radian thường gặp
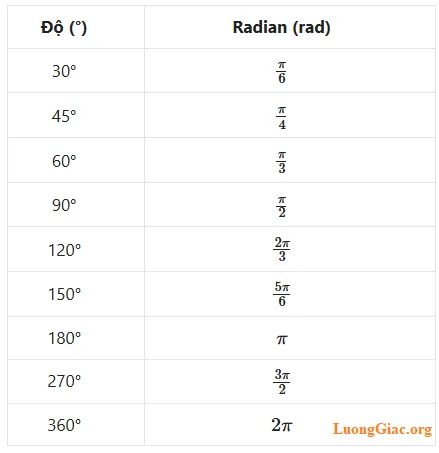
👉 Mẹo nhớ nhanh:
- $180^\circ = \pi$ là cơ sở của mọi phép quy đổi.
- Góc nhân đôi, nhân ba tương ứng nhân với hệ số cùng tỉ lệ trong radian.
5. Ứng dụng của radian trong lượng giác
Radian xuất hiện trong hầu hết các công thức lượng giác chuẩn. Ví dụ:
$\sin(\pi) = 0$
$\cos\left(\frac{\pi}{2}\right) = 0$
$\tan\left(\frac{\pi}{4}\right) = 1$
Khi sử dụng máy tính cầm tay, nếu bạn nhập góc ở đơn vị độ nhưng máy đang ở chế độ RAD (radian), kết quả sẽ sai hoàn toàn.
👉 Luôn kiểm tra ký hiệu “DEG” hoặc “RAD” trên màn hình trước khi tính.
Ví dụ lỗi thường gặp:
- Nếu bạn tính $\sin(30)$ trong chế độ RAD, máy sẽ hiểu $30$ là 30 rad ≈ 1718°, dẫn đến kết quả sai.
- Đúng phải là $\sin(30^\circ)$ hoặc $\sin\left(\frac{\pi}{6}\right)$ trong chế độ DEG hoặc RAD tương ứng.
6. So sánh độ và radian
| Tiêu chí | Độ (°) | Radian (rad) |
|---|---|---|
| Cách định nghĩa | 1 vòng tròn = 360 phần | Cung bằng bán kính → 1 rad |
| Dễ hiểu, dễ hình dung | ✔ | ❌ |
| Ứng dụng | Hình học cơ bản | Toán cao cấp, vật lý, giải tích |
| Sử dụng trong công thức sin, cos | Thường đổi về radian | Là đơn vị chuẩn |
7. Ví dụ
Ví dụ 1: Chuyển $120^\circ$ sang radian:
$120^\circ \times \frac{\pi}{180} = \frac{2\pi}{3}$
Ví dụ 2: Chuyển $\frac{5\pi}{6}$ rad sang độ:
$\frac{5\pi}{6} \times \frac{180}{\pi} = 150^\circ$
Ví dụ 3: Tính độ dài cung khi $r = 5\ \text{cm},\ \alpha = 120^\circ$
Đổi về radian: $\alpha = 120^\circ \times \frac{\pi}{180} = \frac{2\pi}{3}\ \text{rad}$
Khi đó độ dài cung: $l = r\alpha = 5 \times \frac{2\pi}{3} = \frac{10\pi}{3}\ \text{cm}$
8. FAQs
Để chuyển từ độ sang radian, ta sử dụng công thức: $\text{radian} = \text{độ} \times \frac{\pi}{180}$
Ví dụ: $60^\circ = 60 \times \frac{\pi}{180} = \frac{\pi}{3}$.
Công thức này giúp bạn dễ dàng quy đổi góc khi làm bài tập lượng giác.
Bạn cần chuyển đổi khi biểu thức hoặc công thức lượng giác được viết bằng đơn vị khác với đề bài.
Ví dụ: nếu đề bài cho góc bằng độ nhưng công thức yêu cầu góc bằng radian (như khi tính đạo hàm sin, cos), bạn phải đổi sang radian để đảm bảo chính xác.
Có. Hãy ghi nhớ ba giá trị chuẩn: $180^\circ = \pi, \quad 90^\circ = \frac{\pi}{2}, \quad 45^\circ = \frac{\pi}{4}$
Từ đó, bạn có thể suy ra các góc khác nhanh chóng mà không cần bấm máy.
Trong các bài tập cơ bản, độ thường được dùng để mô tả góc hình học.
Còn trong các công thức giải tích như đạo hàm, tích phân hoặc chuyển động tròn, radian là đơn vị bắt buộc vì nó giúp kết quả chính xác và tự nhiên hơn.
Hai công thức cơ bản bạn cần nhớ:
Từ độ sang radian: $\text{radian} = \text{độ} \times \frac{\pi}{180}$
Từ radian sang độ: $\text{độ} = \text{radian} \times \frac{180}{\pi}$
Đây là nền tảng để học các bài về đồ thị lượng giác và các công thức biến đổi nâng cao.
9. Tổng kết
| Kết luận nhanh | Biểu thức |
|---|---|
| $1\ \text{rad} = \frac{180^\circ}{\pi}$ | ≈ 57,3° |
| $1^\circ = \frac{\pi}{180}$ | rad |
Khi học lượng giác, hãy ưu tiên dùng radian vì tất cả các hàm lượng giác, đạo hàm và tích phân đều định nghĩa theo đơn vị này.
Tham khảo thêm: