1. Giới thiệu chung
Trong lượng giác, đường tròn lượng giác là “cánh cửa” giúp kết nối hình học và đại số, nơi mọi giá trị của $\sin$, $\cos$, $\tan$, và $\cot$ được biểu diễn bằng vị trí của điểm trên mặt phẳng.
Nếu “góc lượng giác” cho ta cách đo độ quay, thì “đường tròn lượng giác” cho ta không gian để nhìn thấy chuyển động của góc đó.
Bài viết này sẽ giúp bạn hiểu rõ đường tròn lượng giác là gì, cấu tạo ra sao, vì sao nó là nền tảng của mọi công thức lượng giác
2. Định nghĩa đường tròn lượng giác là gì?
Đường tròn lượng giác là đường tròn tâm (O(0, 0)) và bán kính (R = 1), được đặt trong mặt phẳng tọa độ (Oxy).
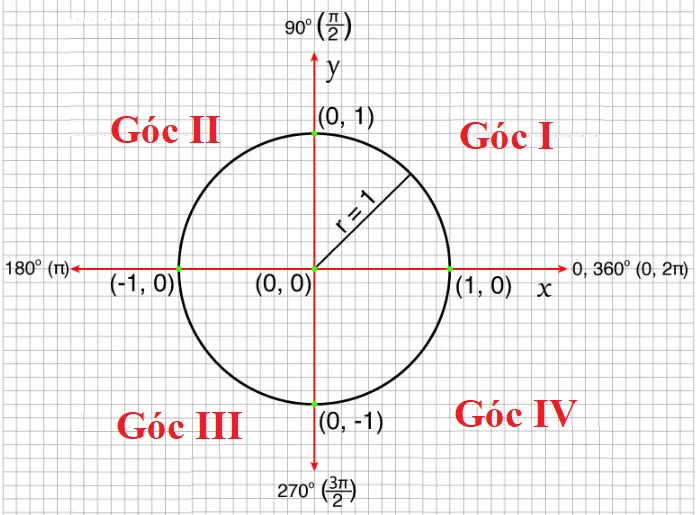
Công thức phương trình tổng quát của đường tròn lượng giác là: $x^2 + y^2 = 1$
Mọi điểm \(M(x, y)\) nằm trên đường tròn này đều thỏa mãn: $x = \cos \alpha, \quad y = \sin \alpha$
Trong đó, α là góc lượng giác (góc quay từ trục \(Ox\) dương đến bán kính \(OM)\).
Điều này có nghĩa: chỉ cần biết góc quay α, ta xác định được toạ độ điểm M – tức là xác định được giá trị sin và cos tương ứng.
3. Cấu trúc và vị trí trên hệ trục tọa độ
Đường tròn lượng giác nằm trên hệ trục (Oxy), chia không gian thành bốn phần tư (quadrants).
Mỗi phần tư tương ứng với dấu của các giá trị sin và cos:
| Phần tư | Miền góc α | Dấu sin α | Dấu cos α |
|---|---|---|---|
| I | \(0^\circ < α < 90^\circ\) | + | + |
| II | \(90^\circ < α < 180^\circ\) | + | – |
| III | \(180^\circ < α < 270^\circ\) | – | – |
| IV | \(270^\circ < α < 360^\circ\) | – | + |
Ví dụ:
- Tại điểm (A(1, 0)): α = 0°, sin α = 0, cos α = 1
- Tại (B(0, 1)): α = 90°, sin α = 1, cos α = 0
- Tại (C(-1, 0)): α = 180°, sin α = 0, cos α = –1
- Tại (D(0, -1)): α = 270°, sin α = –1, cos α = 0
Đây là 4 điểm đặc trưng cơ bản thường dùng trong hầu hết các bài toán lượng giác.
4. Mối liên hệ giữa điểm trên đường tròn và giá trị lượng giác
Với một góc lượng giác α bất kỳ, điểm (M) trên đường tròn lượng giác được xác định bởi: $M(x, y) = (\cos \alpha, \sin \alpha)$
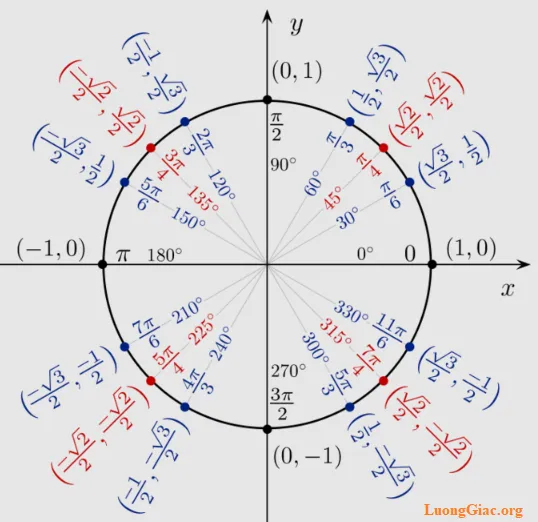
Từ đó, ta có thể tính các giá trị lượng giác cơ bản khác: $\tan \alpha = \frac{\sin \alpha}{\cos \alpha}, \quad \cot \alpha = \frac{\cos \alpha}{\sin \alpha}$
Do đặc tính $x^2 + y^2 = 1$, nên ta có đẳng thức cơ bản của lượng giác:
$\sin^2 \alpha + \cos^2 \alpha = 1$
Đây là công thức Pythagoras trong lượng giác, luôn đúng với mọi giá trị α.
5. Mối quan hệ giữa cung lượng giác và góc lượng giác
Trên đường tròn lượng giác, góc lượng giác α tương ứng với một cung lượng giác có độ dài $l$ được tính bằng công thức:
$l = R \times \alpha$
Trong đó:
- $R$: bán kính đường tròn (với đường tròn lượng giác, $R = 1$)
- $\alpha$: số đo góc lượng giác (tính bằng radian)
Ví dụ:
- Nếu $\alpha = \pi/2$ rad (tức 90°), ta có $l = 1 \times \pi/2 = \pi/2$.
- Nếu $\alpha = \pi$, $l = \pi$.
Cung lượng giác giúp ta biểu diễn chuyển động quay liên tục trên đường tròn, thay vì chỉ các vị trí tĩnh.
6. FAQs
1. Đường tròn lượng giác là gì?
Trả lời:
Đường tròn lượng giác là đường tròn có bán kính bằng 1, tâm tại gốc tọa độ O, dùng để xác định giá trị các hàm lượng giác.
Phương trình của đường tròn lượng giác là:
$x^2 + y^2 = 1$
2. Vì sao bán kính của đường tròn lượng giác bằng 1?
Trả lời:
Vì khi bán kính bằng 1, các giá trị tọa độ của điểm trên đường tròn chính là giá trị của $\sin \theta$ và $\cos \theta$. Điều này giúp việc biểu diễn các hàm lượng giác trở nên trực quan và dễ tính toán.
3. Tâm của đường tròn lượng giác nằm ở đâu?
Trả lời:
Tâm của đường tròn lượng giác luôn nằm tại gốc tọa độ $O(0,0)$ trong hệ trục tọa độ Descartes.
4. Công thức tổng quát của đường tròn lượng giác là gì?
Trả lời:
Phương trình tổng quát của đường tròn lượng giác:
$x^2 + y^2 = 1$
5. Điểm trên đường tròn lượng giác được xác định như thế nào?
Trả lời:
Một điểm $M(x, y)$ thuộc đường tròn lượng giác khi và chỉ khi:
$x = \cos \theta, \quad y = \sin \theta$
với $\theta$ là góc lượng giác xác định vị trí điểm đó.
6. Trục hoành và trục tung trên đường tròn lượng giác có ý nghĩa gì?
Trả lời:
- Trục hoành (Ox): biểu diễn giá trị $\cos \theta$
- Trục tung (Oy): biểu diễn giá trị $\sin \theta$
7. Khi góc lượng giác bằng 0°, điểm M nằm ở đâu trên đường tròn?
Trả lời:
Khi $\theta = 0^\circ$, điểm $M$ nằm tại vị trí $M(1,0)$ — chính là điểm giao của đường tròn với trục Ox.
8. Khi góc lượng giác bằng 90°, điểm M có tọa độ gì?
Trả lời:
Khi $\theta = 90^\circ$, ta có $\cos 90^\circ = 0, \sin 90^\circ = 1$
⟹ Điểm $M(0,1)$ nằm trên trục Oy.
9. Công thức liên hệ giữa sin và cos từ đường tròn lượng giác là gì?
Trả lời:
Từ phương trình đường tròn, ta có đẳng thức cơ bản:
$\sin^2 \theta + \cos^2 \theta = 1$
10. Mỗi điểm trên đường tròn lượng giác biểu diễn điều gì?
Trả lời:
Mỗi điểm $M(x, y)$ trên đường tròn lượng giác biểu diễn một góc lượng giác hoặc một vị trí của góc quay trong mặt phẳng.
11. Hướng quay dương trên đường tròn lượng giác là hướng nào?
Trả lời:
Hướng quay ngược chiều kim đồng hồ được quy ước là hướng dương, còn thuận chiều kim đồng hồ là hướng âm.
12. Liên hệ giữa độ và radian trên đường tròn lượng giác là gì?
Trả lời:
Chu vi đường tròn lượng giác bằng $2\pi$ (radian) tương ứng với $360^\circ$, nên:
$1 \text{ rad} = \frac{180^\circ}{\pi}$
13. Điểm M có tọa độ âm nghĩa là gì?
Trả lời:
Nếu $x < 0$, điểm nằm bên trái trục Oy;
Nếu $y < 0$, điểm nằm dưới trục Ox — tương ứng với góc ở góc phần tư II, III, IV.
14. Tọa độ điểm M tương ứng với góc âm được tính thế nào?
Trả lời:
Khi góc âm $\theta < 0$, điểm $M(\cos \theta, \sin \theta)$ nằm đối xứng qua trục Ox so với điểm có góc $|\theta|$.
15. Công thức tính độ dài cung trong đường tròn lượng giác là gì?
Trả lời:
Nếu góc ở tâm có số đo $\theta$ (radian) và bán kính $r = 1$, thì độ dài cung:
$s = r\theta = \theta$
16. Đường tròn lượng giác giúp xác định giá trị sin và cos như thế nào?
Trả lời:
Giá trị $\sin \theta$ là tung độ (y) và $\cos \theta$ là hoành độ (x) của điểm tương ứng trên đường tròn lượng giác.
17. Điểm trên trục hoành biểu diễn giá trị sin hay cos?
Trả lời:
Điểm trên trục hoành thể hiện giá trị của cosine, còn trên trục tung thể hiện giá trị của sine.
18. Đường tròn lượng giác có đơn vị đo là gì?
Trả lời:
Đường tròn lượng giác thường dùng radian làm đơn vị đo vì công thức lượng giác trở nên đơn giản hơn:
$\text{Cung} = \text{Bán kính} \times \text{Góc (radian)}$
19. Khi góc bằng 180°, tọa độ điểm M là gì?
Trả lời:
Khi $\theta = 180^\circ$:
$\cos 180^\circ = -1, \quad \sin 180^\circ = 0$
⟹ $M(-1, 0)$
20. Khi góc bằng 270°, tọa độ điểm M là gì?
Trả lời:
Khi $\theta = 270^\circ$:
$\cos 270^\circ = 0, \quad \sin 270^\circ = -1$
⟹ $M(0, -1)$
21. Có thể xác định tang và cot từ đường tròn lượng giác không?
Trả lời:
Có.
Với $\theta \neq 90^\circ + k180^\circ$:
$\tan \theta = \frac{\sin \theta}{\cos \theta}, \quad \cot \theta = \frac{\cos \theta}{\sin \theta}$
22. Các góc cùng phương trên đường tròn lượng giác có đặc điểm gì?
Trả lời:
Hai góc cùng phương có các tia trùng nhau, vì vậy tọa độ điểm biểu diễn của chúng giống nhau:
$(\cos \theta, \sin \theta) = (\cos (\theta + k360^\circ), \sin (\theta + k360^\circ))$
23. Góc đối nhau trên đường tròn lượng giác có mối liên hệ ra sao?
Trả lời:
Nếu hai điểm đối nhau qua tâm O thì:
$\cos(\theta + \pi) = -\cos \theta, \quad \sin(\theta + \pi) = -\sin \theta$
24. Vì sao đường tròn lượng giác được dùng trong định nghĩa hàm lượng giác?
Trả lời:
Vì với bán kính $r = 1$, các giá trị lượng giác trở thành tọa độ điểm trên đường tròn, giúp ta định nghĩa sin, cos, tan một cách hình học trực quan.
25. Đường tròn lượng giác giúp mở rộng khái niệm góc như thế nào?
Trả lời:
Đường tròn lượng giác cho phép ta biểu diễn góc lớn hơn 360° hoặc nhỏ hơn 0°, mở rộng khái niệm góc từ hình học sang đại số và lượng giác.
7. Tóm tắt và hướng học tiếp
Tóm lại:
- Đường tròn lượng giác là đường tròn tâm O, bán kính 1.
- Mọi điểm M trên đó có tọa độ $(\cos \alpha, \sin \alpha)$.
- Là cơ sở để xác định, chứng minh và mở rộng toàn bộ hệ thống công thức lượng giác.