Biểu diễn cung lượng giác trên đường tròn lượng giác và hệ thức Chasles là nội dung quan trọng giúp học sinh hình dung trực quan góc lượng giác và mối liên hệ giữa các cung. Dạng toán này thường được sử dụng trong Toán 11 để hỗ trợ so sánh, biến đổi và giải các bài toán lượng giác một cách nhanh và chính xác.
Để biểu diễn cung lượng giác có số đo trên đường tròn lượng giác ta thực hiện như sau:
Chọn điểm $A\left( 1;0 \right)$ làm điểm đầu của cung.
Xác định điểm cuối $M$ của cung sao cho $\overset\frown{AM}=\alpha $
Lưu ý:
- Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của $2\pi $ là: $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=\alpha +k2\pi ;k\in \mathbb{Z}$
- Ngoài ra, ta cũng có thể viết số đo bằng độ: $\text{s }\!\!\tilde{\mathrm{n}}\!\!\text{ }\overset\frown{AM}=x{}^\circ +k360{}^\circ ,k\in \mathbb{Z}$
- Nếu ta có $\overset\frown{AM}=\alpha +k\frac{2\pi }{n};k,n\in \mathbb{Z}$ thì sẽ có $n$ điểm ngọn.
Hệ thức Chasles: Với ba tia $Ou,\,Ov,\,Ow$ bất kì thì ta có: $sd\left( Ou,\,Ov \right)+sd\left( Ov,\,Ow \right)=sd\left( Ou,\,Ow \right)+k{{.360}^{0\,}}\,\,\,\,\,\left( k\in \mathbb{Z} \right)$
Từ đó ta có thể suy ra: $sd\left( Ou,\,Ov \right)=sd\left( Ou,\,Ow \right)-sd\left( Ov,\,Ow \right)+k{{.360}^{0\,}}\,\,\,\,\,\left( k\in \mathbb{Z} \right)$
Câu 1: Một chiếc đồng hồ, có kim chỉ giờ $OG$ chỉ số $9$ và kim phút $OP$ chỉ số$12$. Số đo của góc lượng giác $\left( OG,OP \right)$ là
A. $\frac{\pi }{2}+k2\pi ,\,\,k\in \mathbb{Z}$.
B. $-\,{{270}^{0}}+k{{360}^{0}},\,\,k\in \mathbb{Z}.$
C. ${{270}^{0}}+k{{360}^{0}},\,\,k\in \mathbb{Z}$.
D. $\frac{9\pi }{10}+k2\pi ,\,\,k\in \mathbb{Z}$.
Lời giải
Góc lượng giác $\left( OG,OP \right)$ chiếm $\frac{1}{4}$ đường tròn. Số đo là $\frac{1}{4}.2\pi +k2\pi $, $k\in \mathbb{Z}$.
Câu 2: Trên đường tròn lượng giác có điểm gốc là $A$. Điểm $M$thuộc đường tròn sao cho cung lượng giác $AM$ có số đo ${{45}^{0}}$. Gọi $N$ là điểm đối xứng với $M$ qua trục $Ox$, số đo cung lượng giác $AN$ bằng
A. $-\,\,{{45}^{0}}$.
B. ${{315}^{0}}$.
C. ${{45}^{0}}$ hoặc ${{315}^{0}}$.
D. $-\,\,{{45}^{0}}+k{{360}^{0}},k\in \mathbb{Z}$.
Lời giải
Vì số đo cung $AM$ bằng ${{45}^{0}}$ nên $\widehat{AOM}={{45}^{0}}$, $N$ là điểm đối xứng với $M$ qua trục $Ox$ nên $\widehat{AON}={{45}^{0}}$.
Do đó số đo cung $AN$ bằng ${{45}^{o}}$ nên số đo cung lượng giác $AN$ có số đo là $-\,\,{{45}^{o}}+k{{360}^{o}},\,\,k\in \mathbb{Z}$
Câu 3: Trong hình vẽ bên, ta xem hình ảnh đường tròn trên một bánh lái tàu thuỷ tương ứng với một đường tròn lượng giác.
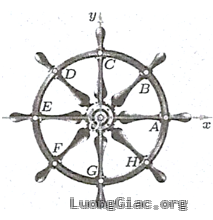
a) Công thức tổng quát biểu diễn góc lượng giác $\left( OA,OB \right)$ theo đơn vị radian:
$\left( OA,OB \right)=\frac{\pi }{4}+k2\pi \left( k\in \mathbb{Z} \right);$
b) Công thức tổng quát chỉ ra góc lượng giác tương ứng với bốn điểm biểu diễn là ${A, C, E, G}$ theo đơn vị radian là $k\frac{\pi }{3}\left( k\in \mathbb{Z} \right)$
c) Công thức tổng quát chỉ ra góc lượng giác tương ứng với hai điểm biểu diễn là ${A, E}$ theo đơn vị độ là $k180{}^\circ \left( k\in \mathbb{Z} \right)$
d) Công thức tổng quát biểu diễn góc lượng giác $\left( OA,OC \right)+\left( OC,OH \right)$ theo đơn vị radian:
$\frac{\pi }{4}+k2\pi \left( k\in \mathbb{Z} \right)$
Lời giải
a) Đúng: Ta có: $\left( OA,OB \right)=\frac{\pi }{4}+k2\pi \left( k\in \mathbb{Z} \right)$;
b) Sai:Ta thấy A, C , E, G lần lượt biểu diễn cho các góc lượng giác: 0 rad; π/2 rad; π rad; 3π/2 rad; ….
Tất cả các góc này theo thứ tự chênh lệch nhau ${\frac{\pi}{2}}$ rad. Vì vậy công thức duy nhất biểu diễn cho các góc lượng giác ấy là ${k \frac{\pi}{2}(k \in \mathbb{Z})}$.
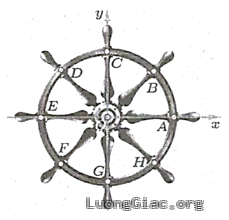
c) Đúng: Ta thấy hai điểm ${A, E}$ lần lượt biểu diễn cho các góc lượng giác ${{0}^{{}^\circ }}{{,180}^{{}^\circ }}{{,360}^{{}^\circ }}{{,540}^{{}^\circ }},..$
Tất cả các góc này theo thứ tự chênh lệch nhau ${180^{\circ}}$. Vì vậy công thức duy nhất biểu diễn cho các góc lượng giác ấy là $k180{}^\circ \left( k\in \mathbb{Z} \right)$.
d) Sai: Theo hệ thức Salơ, ta có:
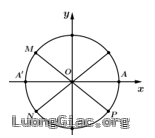
Câu 4: Biết $OM{B}’$ và $ON{B}’$ là các tam giác đều. Cung $\alpha $ có mút đầu là $A$ và mút cuối trùng với $B$ hoặc $M$ hoặc$N$. Tính số đo của $\alpha $?
Lời giải
$\begin{align}
& \left( OA,OB \right)+\left( OB,OC \right)=\left( OA,OC \right)=\frac{\pi }{2}+k2\pi \left( k\in \mathbb{Z} \right) \\
& \left( OA,OC \right)+\left( OC,OH \right)=\left( OA,OH \right)=-\frac{\pi }{4}+k2\pi \left( k\in \mathbb{Z} \right) \\
\end{align}$
Cung $\alpha $ có mút đầu là $A$ và mút cuối trùng với $B$nên $\alpha =\frac{\pi }{2}$.
Cung $\overset\frown{AM}=\overset\frown{AB}+\,\frac{2\pi }{3}$, $\overset\frown{AN}=\overset\frown{AM}+\,\frac{2\pi }{3}$ nên chu kì của cung $\alpha $ là $\frac{2\pi }{3}$.
Câu 5: Trên đường tròn lượng giác có điểm gốc là $A$. Điểm $M$ thuộc đường tròn sao cho cung lượng giác $AM$ có số đo ${{45}^{0}}$. Gọi $N$ là điểm đối xứng với $M$ qua trục $Ox$, số đo cung lượng giác $AN$ bằng bao nhiêu?
Lời giải
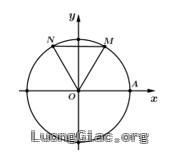
Vì số đo cung $\overset\frown{AM}$ bằng ${{45}^{0}}$ nên $\widehat{AOM}={{45}^{0}}$, $N$ là điểm đối xứng với $M$ qua trục $Ox$ nên $\widehat{AON}={{45}^{0}}$.
Do đó số đo cung $AN$ bằng ${{45}^{0}}$ nên số đo cung lượng giác $AN$ có số đo là $-{{45}^{0}}+k{{360}^{0}},\,k\in \mathbb{Z}$
Skip to PDF content