Giải bài tập tìm giá trị lượng giác của góc lượng giác là dạng toán cơ bản nhưng rất quan trọng trong Toán 11, giúp học sinh nắm chắc cách xác định sin, cos, tan, cot của một góc bất kỳ. Nội dung này là nền tảng để giải phương trình, bất phương trình và các bài toán lượng giác nâng cao.
Phương pháp: Sử dụng nhóm công thức liên hệ giữa các giá trị lượng giác để tính toán
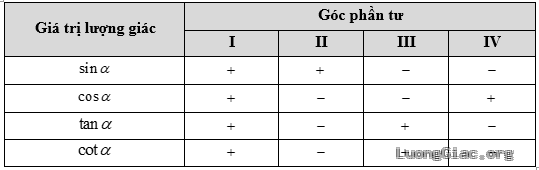
Chú ý: Nếu đề bài có giới hạn miền của góc $\alpha $ thì ta cần xem trên miền đó các tỉ số lượng giác tương ứng sẽ mang dấu như thế nào, cụ thể như sau:
Câu 1: Trong các hệ thức sau đây, hệ thức nào đúng?
A. $\sin {{x}^{2}}+\cos {{x}^{2}}=1$
B. $\sin x+\cos x=1$
C. $\sin 2x+\cos 2x=1$.
D. ${{\sin }^{2}}x+\cos {{x}^{2}}=1$.
Lời giải
Theo công thức: $\sin {{x}^{2}}+\cos {{x}^{2}}=1$.
Câu 2: Cho $2\pi <\alpha <\frac{5\pi }{2}.$ Khẳng định nào sau đây đúng?
A. $\tan \alpha >0;\text{ }\cot \alpha >0.$
B. $\tan \alpha <0;\text{ }\cot \alpha <0.$
C. $\tan \alpha >0;\text{ }\cot \alpha <0.$
D. $\tan \alpha <0;\text{ }\cot \alpha >0.$
Lời giải
Ta có $2\pi <\alpha <\frac{5\pi }{2}\Rightarrow $điểm cuối cung $\alpha -\pi $ thuộc góc phần tư thứ $I$$\Rightarrow \left\{ \begin{align}
& \tan \alpha >0 \\
& \cot \alpha >0 \\
\end{align} \right..$
Câu 3: Cho $\frac{\pi }{2}<\alpha <\pi .$ Giá trị lượng giác nào sau đây luôn dương?
A. $\sin \left( \pi +\alpha \right).$
B. $\cot \left( \frac{\pi }{2}-\alpha \right).$
C. $\cos \left( -\alpha \right).$
D. $\tan \left( \pi +\alpha \right).$
Lời giải
$\sin \left( \pi +\alpha \right)=-\sin \alpha ;$ $\cot \left( \frac{\pi }{2}-\alpha \right)=\sin \alpha ;$ $\cos \left( -\alpha \right)=\cos \alpha ;$ $\tan \left( \pi +\alpha \right)=\tan \alpha .$
Do $\frac{\pi }{2}<\alpha <\pi \Rightarrow \left\{ \begin{align} & \sin \alpha >0 \\ & \cos \alpha <0 \\ & \tan \alpha <0 \\ \end{align} \right.$
Câu 4: Đơn giản biểu thức $A=\cos \left( \alpha -\frac{\pi }{2} \right)$, ta được:
A. $\cos \alpha $.
B. $\sin \alpha $.
C. $\cos \alpha $.
D. $-\sin \alpha $.
Lời giải
Ta có: $A=\cos \left( \alpha -\frac{\pi }{2} \right)$$=\cos \left( \frac{\pi }{2}-\alpha \right)$$=\sin \alpha $.
Câu 5: Tính được các giá trị lượng giác của góc $\alpha =\frac{\pi }{3}+k2\pi $$\left( k\in \mathbb{Z} \right)$. Xét tính đúng sai của các khẳng định sau:
a) $\sin \alpha =-\frac{\sqrt{3}}{2}$
b) $\cos \alpha =-\frac{1}{2}$
c) $\tan \alpha =\sqrt{3}$
d) $\cot \alpha =-\frac{\sqrt{3}}{3}$
Lời giải
a) Sai: $\sin \left( \frac{\pi }{3}+k2\pi \right)=\sin \frac{\pi }{3}=\frac{\sqrt{3}}{2}$
b) Sai: $\cos \left( \frac{\pi }{3}+k2\pi \right)=\cos \frac{\pi }{3}=\frac{1}{2}$
c) Đúng: $\tan \left( \frac{\pi }{3}+k2\pi \right)=\tan \frac{\pi }{3}=\sqrt{3}$
d) Sai: $\cot \left( \frac{\pi }{3}+k2\pi \right)=\cot \frac{\pi }{3}=\frac{\sqrt{3}}{3}$
Câu 6: Tính được các giá trị lượng giác còn lại của góc $x$ biết: $\cos x=-\frac{5}{13}$ với $180{}^\circ <x<270{}^\circ $. Xét tính đúng sai của các khẳng định sau:
a) $\sin x<0$
b) $\tan x=\frac{12}{5}$
c) $\cot x=\frac{5}{12}$
d) $\sin x-\cos x=-\frac{12}{13}$
Lời giải
a) Đúng: Do ${{180}^{{}^\circ }}<x<{{270}^{{}^\circ }}\Rightarrow \sin x<0$
b) Đúng: Ta có: ${\sin ^2}x + {\cos ^2}x = 1$ $ \Rightarrow {\sin ^2}x = 1 – {\cos ^2}x = 1 – \frac{{25}}{{169}} = \frac{{144}}{{169}}$ $ \Rightarrow \sin x = – \frac{{12}}{{13}};$ $\tan x = \frac{{\sin x}}{{\cos x}} = \frac{{12}}{5}$
c) Đúng: $\cot x=\frac{\cos x}{\sin x}=\frac{5}{12}$
d) Sai: $\sin x-\cos x=-\frac{7}{13}$
Câu 7: Cho góc $\alpha $ thỏa mãn $\cos \alpha =-\frac{\sqrt{5}}{3}$ và $\pi <\alpha <\frac{3\pi }{2}$. Tính $\tan \alpha .$
Lời giải
Ta có $\left\{ \begin{array}{l} \sin \alpha = \pm \sqrt {1 – {{\cos }^2}\alpha } = \pm \frac{2}{3}\\ \pi < \alpha < \frac{{3\pi }}{2} \end{array} \right.$ $ \to sin\alpha = – \frac{2}{3}$ $ \to \tan \alpha = \frac{{sin\alpha }}{{\cos \alpha }} = \frac{2}{{\sqrt 5 }} \approx 0,89$
Câu 8: Thanh $OM$ quay ngược chiều kim đồng hồ quanh gốc $O$ của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như hình bên. Vị trí ban đầu của thanh là $OA$. Hỏi độ dài bóng ${O}’M$ của $OM$ khi thanh quay được $\frac{60}{13}$ vòng là bao nhiêu, biết độ dài thanh $OM$ là $10\text{ }\!\!~\!\!\text{ cm}$? Kết quả làm tròn đến hàng phần mười.
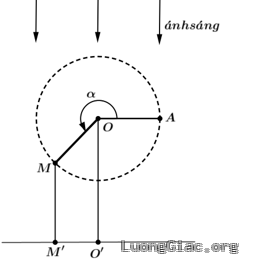
Lời giải
Ta có $\alpha =\frac{60}{13}\cdot 2\pi =\frac{120\pi }{13}$. Suy ra ${O}'{M}’=\left| OM\text{cos}\alpha \right|=\left| 10\text{cos}\frac{120\pi }{13} \right|\approx 7,5\text{ }\!\!~\!\!\text{ cm}$.
Skip to PDF content