1. Giới thiệu về góc lượng giác
Trong hình học cổ điển, một góc được hiểu là phần mặt phẳng được tạo bởi hai tia chung gốc. Tuy nhiên, trong lượng giác học hiện đại, khái niệm này được mở rộng thành góc lượng giác – cho phép ta mô tả không chỉ độ mở giữa hai tia, mà còn hướng quay và số vòng quay.
Góc lượng giác là nền tảng để định nghĩa giá trị lượng giác của một góc, đường tròn lượng giác, và các đẳng thức lượng giác cơ bản. Vì vậy, hiểu rõ bản chất của góc lượng giác là bước đầu tiên để học tốt toàn bộ chương “Lượng giác”.
2. Khái niệm góc lượng giác
2.1. Định nghĩa
Một góc lượng giác được xác định bởi một tia ban đầu (gọi là tia gốc) và một tia cuối, cùng gốc \( O \), đồng thời có kèm chiều quay từ tia gốc đến tia cuối.
Ta ký hiệu góc lượng giác là \( (OM, ON) \), trong đó:
- \( OM \): tia gốc
- \( ON \): tia cuối
- Gốc quay: điểm \( O \)
Khi tia ( ON ) trùng với tia ( OM ), ta có góc lượng giác bằng 0: $\alpha = 0$
2.2. Hướng quay
- Nếu tia \( ON \) quay ngược chiều kim đồng hồ, ta nói góc lượng giác đó là dương.→ Ví dụ: $ \alpha = +60^\circ $
- Nếu tia \( ON \) quay cùng chiều kim đồng hồ, ta nói góc lượng giác đó là âm.→ Ví dụ: $ \alpha = -60^\circ $
Như vậy, khác với “góc hình học” chỉ nhận giá trị dương từ \( 0^\circ \) đến \( 180^\circ \), góc lượng giác có thể nhận mọi giá trị thực, tức: $\alpha \in \mathbb{R}$
3. Đơn vị đo góc lượng giác
3.1. Độ (Degree)
Đơn vị độ thường dùng trong hình học phổ thông:
- Một vòng tròn tương ứng với \( 360^\circ \).
- Một độ chia thành \( 60 \) phút, và mỗi phút chia thành \( 60 \) giây.
Ký hiệu: $1^\circ = 60′ = 3600”$
3.2. Radian
Trong lượng giác, đơn vị quan trọng hơn là radian, vì nó giúp các công thức trở nên tự nhiên và gọn hơn khi chuyển sang đại số hoặc giải tích.
Một radian là góc ở tâm chắn cung có độ dài bằng bán kính của đường tròn: $1 \text{ radian} = \text{góc chắn cung } s = R$
Mối liên hệ giữa độ và radian: $ 180^\circ = \pi \text{ radian} $ hay tương đương: $ 1^\circ = \frac{\pi}{180} \text{ rad}, \quad 1 \text{ rad} = \frac{180}{\pi}^\circ $
Ví dụ:
- \( 90^\circ = \frac{\pi}{2} \text{ rad} \)
- \( 60^\circ = \frac{\pi}{3} \text{ rad} \)
- \( 45^\circ = \frac{\pi}{4} \text{ rad} \)
- \( 360^\circ = 2\pi \text{ rad} \)
Để nắm vững hơn mối quan hệ giữa độ và radian, bạn có thể tham khảo bài viết “Chuyển đổi giữa độ và radian trong lượng giác”. Bài viết sẽ giúp bạn hiểu rõ cách hai đơn vị này liên kết với nhau và cách vận dụng chúng hiệu quả trong các bài toán thực tế.
4. Cách biểu diễn góc lượng giác
4.1. Trên mặt phẳng tọa độ
Trong hệ trục tọa độ \( Oxy \), ta thường chọn:
- Tia \( Ox \) làm tia gốc của góc lượng giác.
- Chiều quay ngược kim đồng hồ là chiều dương.
Như vậy, một điểm \( M \) bất kỳ trên đường tròn lượng giác (bán kính \( R = 1 \)) xác định một góc lượng giác \( \alpha \) với: $ \alpha = (Ox, OM) $
4.2. Góc lượng giác có cùng tia cuối
Hai góc lượng giác được gọi là cùng phương hoặc đồng vị nếu tia cuối của chúng trùng nhau.
Giả sử ta có hai góc: $\alpha = (OM, ON), \quad \beta = (OM, ON’)$
Nếu \( ON’ \) trùng với \( ON \) sau \( k \) vòng quay (với \( k \in \mathbb{Z} )\), ta có: $\beta = \alpha + k \times 360^\circ = \alpha + 2k\pi \text{ (radian)}$
Ví dụ:
- Các góc \( 30^\circ, 390^\circ, -330^\circ \) đều có cùng tia cuối.
- Tập hợp các góc cùng tia cuối với góc \( \alpha \) là:${ \alpha + 2k\pi \mid k \in \mathbb{Z} }$
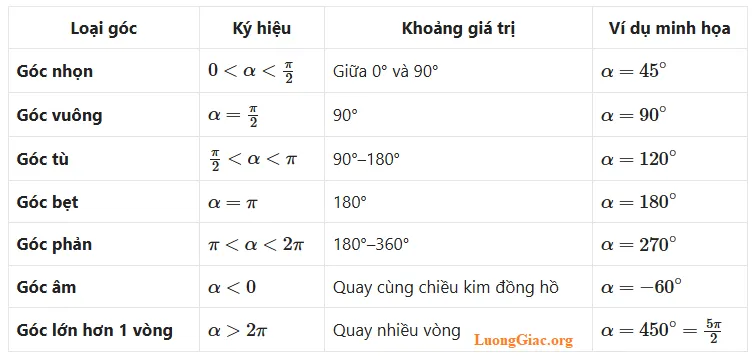
5. Phân loại góc lượng giác theo giá trị
6. Ví dụ minh họa
Ví dụ 1. Tính số đo radian của góc \( 225^\circ \).
Giải:
$225^\circ = 225 \times \frac{\pi}{180} = \frac{5\pi}{4} \text{ rad}$
Ví dụ 2. Tìm các góc cùng phương với \( \alpha = 30^\circ \) có số đo trong khoảng \([-360^\circ, 720^\circ]\).
Giải:
$\alpha_k = 30^\circ + 360^\circ \times k, \quad k \in \mathbb{Z}$
Khi đó:
- Với \( k = -1 \Rightarrow \alpha = -330^\circ \)
- Với \( k = 0 \Rightarrow \alpha = 30^\circ \)
- Với \( k = 1 \Rightarrow \alpha = 390^\circ \)
- Với \( k = 2 \Rightarrow \alpha = 750^\circ \) (loại vì vượt 720°)
⟹ Các góc thỏa mãn là: −330°, 30°, 390°.
7. Ý nghĩa của góc lượng giác trong lượng giác học
Góc lượng giác giúp ta:
- Mô tả các giá trị sin, cos, tan trên toàn trục số thực (không giới hạn trong 0°–180°).
- Hiểu được chu kỳ của các hàm lượng giác: $ \sin(\alpha + 2k\pi) = \sin\alpha, \quad \cos(\alpha + 2k\pi) = \cos\alpha $
- Kết nối hình học phẳng với hàm số lượng giác, mở đường cho việc học giải tích lượng giác ở cấp độ cao hơn.
8. Câu hỏi thường gặp
1. Góc lượng giác là gì?
→ Là góc được xác định bởi một tia gốc, một tia quay và chiều quay (dương hoặc âm).
2. Góc lượng giác khác góc hình học như thế nào?
→ Góc hình học chỉ có giá trị dương trong khoảng $0^\circ$ đến $180^\circ$, còn góc lượng giác có thể âm, lớn hơn $360^\circ$ hoặc nhỏ hơn $0^\circ$.
3. Tia gốc của góc lượng giác là gì?
→ Là tia cố định ban đầu (thường chọn trùng với trục $Ox$) trong mặt phẳng tọa độ.
4. Tia cuối của góc lượng giác là gì?
→ Là vị trí của tia sau khi quay từ tia gốc một góc $\alpha$ nhất định.
5. Khi nào góc lượng giác dương?
→ Khi tia quay ngược chiều kim đồng hồ, ta có $\alpha > 0$.
6. Khi nào góc lượng giác âm?
→ Khi tia quay cùng chiều kim đồng hồ, ta có $\alpha < 0$.
7. Góc lượng giác bằng 0 khi nào?
→ Khi tia cuối trùng với tia gốc, tức $\alpha = 0$.
8. Đơn vị đo góc lượng giác là gì?
→ Có hai đơn vị phổ biến: độ ($^\circ$) và radian (rad).
9. 1 radian bằng bao nhiêu độ?
→ $1\text{ rad} = \frac{180}{\pi}^\circ$
10. 1 độ bằng bao nhiêu radian?
→ $1^\circ = \frac{\pi}{180}\text{ rad}$
11. Công thức đổi độ sang radian là gì?
→ $\alpha_{\text{rad}} = \alpha_{\text{độ}} \times \frac{\pi}{180}$
12. Công thức đổi radian sang độ là gì?
→ $\alpha_{\text{độ}} = \alpha_{\text{rad}} \times \frac{180}{\pi}$
13. Một vòng quay tương ứng với bao nhiêu radian?
→ Một vòng đầy có $360^\circ = 2\pi$ rad.
14. Góc cùng phương là gì?
→ Là các góc có cùng tia cuối, khác nhau $360^\circ \times k$ hoặc $2\pi k$ rad, với $k \in \mathbb{Z}$.
15. Ví dụ các góc cùng phương?
→ $30^\circ$, $390^\circ$ và $-330^\circ$ là các góc cùng phương vì khác nhau $360^\circ$.
16. Công thức tổng quát góc cùng phương là gì?
→ $\alpha’ = \alpha + 2k\pi$ (rad) hoặc $\alpha’ = \alpha + 360^\circ k$ (độ), với $k \in \mathbb{Z}$.
17. Các loại góc trong lượng giác là gì?
→ Góc nhọn $(0 < \alpha < \frac{\pi}{2})$, vuông $(\alpha = \frac{\pi}{2})$, tù $(\frac{\pi}{2} < \alpha < \pi)$, bẹt $(\alpha = \pi)$, phản $(\pi < \alpha < 2\pi)$ và góc âm $(\alpha < 0)$.
18. Góc lượng giác có thể lớn hơn $360^\circ$ không?
→ Có, vì nó biểu diễn số vòng quay của tia, không giới hạn trong một chu kỳ.
19. Độ dài cung lượng giác được tính thế nào?
→ $s = R\alpha$ (với $\alpha$ tính bằng radian).
20. Giá trị của góc lượng giác thuộc miền nào?
→ $\alpha \in \mathbb{R}$, tức có thể nhận mọi giá trị thực.
21. Góc $180^\circ$ bằng bao nhiêu radian?
→ $180^\circ = \pi$ rad.
22. Góc $90^\circ$ bằng bao nhiêu radian?
→ $90^\circ = \frac{\pi}{2}$ rad.
23. Góc $270^\circ$ bằng bao nhiêu radian?
→ $270^\circ = \frac{3\pi}{2}$ rad.
24. Góc lượng giác và cung lượng giác khác nhau thế nào?
→ Góc lượng giác thể hiện độ quay của tia, còn cung lượng giác thể hiện độ dài cung tương ứng trên đường tròn lượng giác.
25. Góc lượng giác dùng để làm gì trong toán học?
→ Để xác định các giá trị lượng giác $\sin\alpha$, $\cos\alpha$, $\tan\alpha$ và mô tả các hiện tượng tuần hoàn.